题目内容
18．
如图，直线a是一个轴对称图形的对称轴，画出这个轴对称图形的另一半，并说明这个轴对称图形是一个什么图形，它一共有几条对称轴．
分析 利用轴对称图形的性质结合等边三角形的判定方法进而得出答案．
解答 
解：如图所示：△ABC即为所求，
这个轴对称图形是等边三角形，它一共有3条对称轴．
点评 此题主要考查了作轴对称变换以及等边三角形的性质，正确得出图形的形状是解题关键．
练习册系列答案
相关题目
8．在△ABC中，若∠A：∠B：∠C=4：3：1，则△ABC是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 钝角三角形 | D． | 无法确定 |
9．-$\frac{1}{2}$的倒数，相反数分别是（ ）
| A． | 2，2 | B． | -2，$\frac{1}{2}$ | C． | $\frac{1}{2}$，$\frac{1}{2}$ | D． | -$\frac{1}{2}$，-2 |
13．某厂的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3小时后安排2人装箱，若3小时装产品150件，未装箱的产品数量（y）是时间（t）的函数，这个函数的大致图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
10．下列交换加数的位置的变形中，正确的是（ ）
| A． | 1-2+3-4=1+3-2+4 | B． | 1-2+3-4=1-3-2+4 | C． | 1-2+3-4=1+3-2-4 | D． | 1-2+3-4=1-3+2-4 |
7．
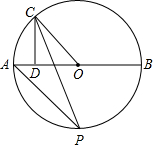如图，AB为⊙O的直径，C为⊙O上半圆一动点（不与A、B重合），CD⊥AB于D，∠OCD的平分线交⊙O于点P，则当点C在⊙O上运动时，点P的位置（ ）
如图，AB为⊙O的直径，C为⊙O上半圆一动点（不与A、B重合），CD⊥AB于D，∠OCD的平分线交⊙O于点P，则当点C在⊙O上运动时，点P的位置（ ）| A． | 随点C的运动而改变 | B． | 不变 | ||
| C． | 在是PA=OA的劣弧上 | D． | 无法确定 |
如图，要建一个面积为130m2的仓库，仓库的一边靠墙（墙长16米），并在与墙平行的一边开一道1米宽的门．现有能围成32米长的木板，求仓库的长和宽．