题目内容
2. 如图,AD是△ABC的角平分线,∠B=50°,∠ADC=70°,求∠BAC、∠C的度数.
如图,AD是△ABC的角平分线,∠B=50°,∠ADC=70°,求∠BAC、∠C的度数.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BAD,再根据角平分线的定义可得∠BAC=2∠BAD,然后利用三角形的内角和定理列式计算即可求出∠C.
解答 解:∵∠B=50°,∠ADC=70°,
∴∠BAD=∠ADC-∠B=70°-50°=20°,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×20°=40°,
在△ABC中,∠C=180°-∠BAC-∠B=180°-50°-40°=90°.
点评 本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,三角形内角和定理,是基础题,准确识图是解题的关键.

练习册系列答案
相关题目
12.下列说法中,错误的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线平分对角的平行四边形是菱形 | |
| C. | 四个内角相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
13.某厂的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排2人装箱,若3小时装产品150件,未装箱的产品数量(y)是时间(t)的函数,这个函数的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列交换加数的位置的变形中,正确的是( )
| A. | 1-2+3-4=1+3-2+4 | B. | 1-2+3-4=1-3-2+4 | C. | 1-2+3-4=1+3-2-4 | D. | 1-2+3-4=1-3+2-4 |
17.设a=2$\sqrt{2}$,b=$\frac{1}{a}$,则a、b的大小关系是( )
| A. | a=b | B. | a>b | C. | a<b | D. | a>-b |
7.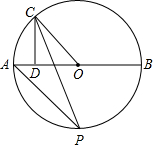 如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
 如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )
如图,AB为⊙O的直径,C为⊙O上半圆一动点(不与A、B重合),CD⊥AB于D,∠OCD的平分线交⊙O于点P,则当点C在⊙O上运动时,点P的位置( )| A. | 随点C的运动而改变 | B. | 不变 | ||
| C. | 在是PA=OA的劣弧上 | D. | 无法确定 |
11. 如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
 如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )
如图,在△ABC中,AB=AC,D是BC延长线上的一点,∠A=40°,则∠ACD等于( )| A. | 80° | B. | 100° | C. | 110° | D. | 120° |
 如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.
如图,△ABC中,AB=AC,∠BAC与∠BCA的平分线AD、CD交于点D,若∠BAC=80°,则∠ADC=115°.