题目内容
1.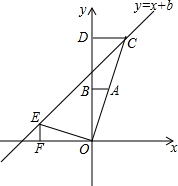 如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).
如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).(1)分别写出点C、E的坐标C(2,2t),E(-t,1)(用含t的代数式表示);
(2)如果直线y=x+b经过E、C两点,试求出t与b的值.
分析 (1)根据位似变换的性质求出CD与AB、OD与OB的关系,得到点C的坐标,根据旋转的性质求出OF与OB、EF与AB的关系,得到点E的坐标;
(2)用待定系数法求出t与b的值.
解答 解:(1)由位似变换的性质可知,CD=2AB、OD=2OB,
∵点A的坐标是(1,t),
∴点C的坐标(2,2t),
由旋转的性质可知,OF=OB、EF=AB,
∴点E的坐标(-t,1);
(2)由题意得,
$\left\{\begin{array}{l}{2+b=2t}\\{-t+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{t=3}\\{b=4}\end{array}\right.$.
点评 本题考查的是一次函数的性质、位似变换的性质和旋转的性质,能够根据位似变换的性质和旋转的性质确定对应线段之间的位置关系和数量关系是解题的关键,注意待定系数法求解析式的正切运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
6.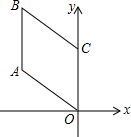 如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
 如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )| A. | (-2,2+$\sqrt{2}$) | B. | (2,2+$\sqrt{2}$) | C. | ($-\sqrt{2}$,2+$\sqrt{2}$) | D. | ($\sqrt{2}$,2+$\sqrt{2}$) |
11.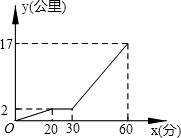 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )| A. | 小强从家到公共汽车站步行了2公里 | |
| B. | 小强在公共汽车站等小明用了10分钟 | |
| C. | 公共汽车的平均速度是30公里/小时 | |
| D. | 小强乘公共汽车用了20分钟 |
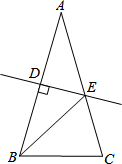 如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.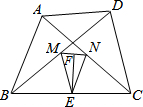 如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.
如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.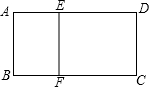 如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.
如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.