题目内容
2. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
分析 根据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.
解答 解:∵CC′∥AB,
∴∠ACC′=∠CAB=65°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°-2∠ACC′=180°-2×65°=50°,
∴∠CAC′=∠BAB′=50°.
故选C.
点评 本题考查了旋转的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知一个函数图象经过(1,-4),(2,-2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是( )
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
11.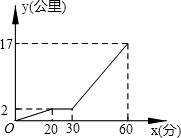 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )| A. | 小强从家到公共汽车站步行了2公里 | |
| B. | 小强在公共汽车站等小明用了10分钟 | |
| C. | 公共汽车的平均速度是30公里/小时 | |
| D. | 小强乘公共汽车用了20分钟 |
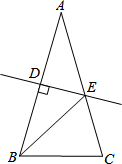 如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.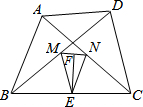 如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.
如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.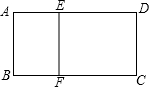 如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.
如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.

 如图,AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数.
如图,AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数.