题目内容
3.在一次“探究性学习”课中,老师设计如下数表:| n | 2 | 3 | 4 | 5 | 6 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | 62-1 | … |
| b | 4 | 6 | 8 | 10 | 12 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | 62+1 | … |
(2)用含自然数n(n>1)的代数式表示a、b、c,则a=n2-1,b=2n,c=n2+1.
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
分析 (1)观察表格,即可得出n=6时a、b、c的值;
(2)利用图表可以发现a,b,c与n的关系,a与c正好是n2,加减1,即可得出答案;
(3)利用完全平方公式计算出a2+b2的值,以及c2的值,再利用勾股定理逆定理即可求出.
解答 解:(1)由图表可以得出:
∵n=2时,a=22-1,b=2×2,c=22+1,
n=3时,a=32-1,b=2×3,c=32+1,
n=4时,a=42-1,b=2×4,c=42+1,
n=5时,a=52-1,b=2×5,c=52+1,
∴n=6时,a=62-1,b=12,c=62+1;
(2)a=n2-1,b=2n,c=n2+1;
(3)以a,b,c为边的三角形是直角三角形.理由如下:
∵a2+b2=(n2-1)+(2n)2=n4-2n2+1+4n2=(n2+1)2=c2,
∴以a,b,c为边的三角形是直角三角形.
故答案为62-1,12,62+1;n2-1,2n,n2+1.
点评 本题考查了勾股定理的逆定理,解题的关键是仔细观察表中的数据,找出规律,进而利用勾股定理的逆定理解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在平面直角坐标系中,点P的横坐标是3,且点P到x轴的距离为5,则点P的坐标是( )
| A. | (3,5) | B. | (3,-5) | C. | (3,5)或(3,-5) | D. | (-3,5)或(-3,-5) |
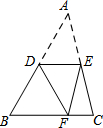 如图,△ABC的中位线DE=5,把△ABC沿DE折叠,使点A落在边BC上的点F处,且AF=8,则BC=10,△ABC的面积为40.
如图,△ABC的中位线DE=5,把△ABC沿DE折叠,使点A落在边BC上的点F处,且AF=8,则BC=10,△ABC的面积为40. 如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.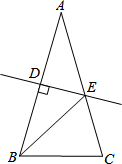 如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.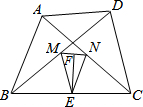 如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.
如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.