题目内容
已知圆内接正方形边长为m,求该圆外切正三角形边长.
考点:正多边形和圆
专题:
分析:如图,作辅助线;根据勾股定理首先求出EG的长度,进而得到EO的长度;根据直角三角形的边角关系求出AE的长度,即可解决问题.
解答: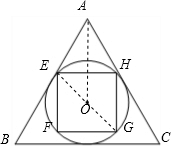 解:如图,连接GE、OA;则GE必过点O;
解:如图,连接GE、OA;则GE必过点O;
∵△ABC为⊙O的外切正三角形,
∴OE⊥AB,∠OAE=∠OAH=
×60°=30°;
∵四边形EFGH为⊙O的内接正方形,
∴EF=FG=m,∠EFG=90°,
由勾股定理得:EG2=EF2+FG2=2m2,
∴EG=
m,EO=
;
在直角△AOE中,
∵tan30°=
,
∴AE=
m;同理可求BE=
m,
∴AB=
m,
即该圆外切正三角形边长为
m.
 解:如图,连接GE、OA;则GE必过点O;
解:如图,连接GE、OA;则GE必过点O;∵△ABC为⊙O的外切正三角形,
∴OE⊥AB,∠OAE=∠OAH=
| 1 |
| 2 |
∵四边形EFGH为⊙O的内接正方形,
∴EF=FG=m,∠EFG=90°,
由勾股定理得:EG2=EF2+FG2=2m2,
∴EG=
| 2 |
| ||
| 2 |
在直角△AOE中,
∵tan30°=
| OE |
| AE |
∴AE=
| ||
| 2 |
| ||
| 2 |
∴AB=
| 6 |
即该圆外切正三角形边长为
| 6 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了一定的要求

练习册系列答案
相关题目
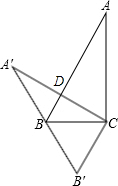 在Rt△ABC中,∠ACB=90°,∠ABC=60°,将△ABC绕顶点C旋转到△A′B′C′的位置,使点B恰落在斜边A′B′上,设AC与AB相交于点D,则∠BDC=( )
在Rt△ABC中,∠ACB=90°,∠ABC=60°,将△ABC绕顶点C旋转到△A′B′C′的位置,使点B恰落在斜边A′B′上,设AC与AB相交于点D,则∠BDC=( )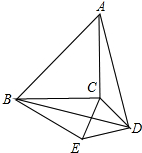 如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.