Question

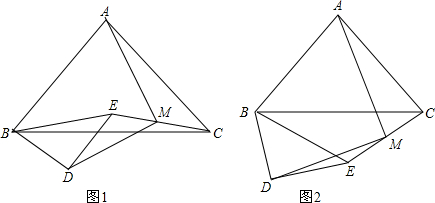
如图，在△ABC、△DBE中，已知AC=AB，DE=DB，∠BAC=∠EDB=90°，连接CE
（1）如图1，取CE的中点M，连接AM、DM，则AM、DM之间有何关系？并给予证明；
（2）当△DBE绕点B旋转到如图2位置时，其他条件不变，则（1）中的结论是否成立？请证明．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）过A作AN⊥BC，过D作DF⊥BE，连接MF，MN．易证∠DFM=∠ANM，DF=MN，FM=AN，即可证明△DFM≌△MNA，可得DM=AM，∠DMF=∠MAN，根据AN⊥FM即可求得∠AMD=90°，即可解题；
（2）过A作AN⊥BC，过D作DF⊥BE，连接MF，MN．易证∠DFM=∠ANM，DF=MN，FM=AN，即可证明△DFM≌△MNA，可得DM=AM，∠DMF=∠MAN，根据AN⊥FM即可求得∠AMD=90°，即可解题．

解答：证明：（1）过A作AN⊥BC，过D作DF⊥BE，连接MF，MN．

∵△ABC和△BDE均为等腰RT△，
∴F是BE中点，N是BC中点，
∴MF=

1

2

BC，MN=

1

2

BE，DF=

1

2

BE，AN=

1

2

BC，
∵MN∥BE，FM∥BC，
∴∠CNM=∠CBE=∠MFE，
∵∠DFM+∠MFE=90°，∠ANM+∠CNM=90°，
∴∠DFM=∠ANM，
∵在△DFM和△MNA中，

DF=MN ∠DFM=∠ANM FM=AN

，
∴△DFM≌△MNA，（SAS）
∴DM=AM，∠DMF=∠MAN，
∵AN⊥BC，FM∥BC，
∴AN⊥FM，
∵∠MAN+∠AMF=90°，
∴∠DMF+∠AMF=90°，
∴∠AMD=90°，即AM⊥DM；
（2）过A作AN⊥BC，过D作DF⊥BE，连接MF，MN．

∵△ABC和△BDE均为等腰RT△，
∴F是BE中点，N是BC中点，
∴MF=

1

2

BC，MN=

1

2

BE，DF=

1

2

BE，AN=

1

2

BC，
∵MN∥BE，FM∥BC，
∴∠CNM=∠CBE=∠MFE，
∵∠DFM=∠MFE+90°，∠ANM=∠CNM+90°，
∴∠DFM=∠ANM，
∵在△DFM和△MNA中，

DF=MN ∠DFM=∠ANM FM=AN

，
∴△DFM≌△MNA，（SAS）
∴DM=AM，∠DMF=∠MAN，
∵AN⊥BC，FM∥BC，
∴AN⊥FM，
∵∠MAN+∠AMF=90°，
∴∠DMF+∠AMF=90°，
∴∠AMD=90°，即AM⊥DM．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△DFM≌△MNA是解题的关键．