题目内容
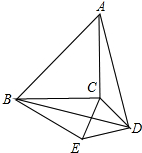 如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.(1)求∠BCE的大小;
(2)求证:BE=AC.
考点:全等三角形的判定与性质,等边三角形的性质,等腰直角三角形
专题:
分析:(1)根据等腰三角形的性质得出AC=BC,∠CAB=∠CBA=45°根据等边三角形的性质得出AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°求出∠DAC=15°,∠DBC=15°,∠EDB=∠CDA,根据SAS推出△ADC≌△BDE,推出BE=AC=BC,∠EBD=∠CAD=15°即可;
(2)根据全等三角形的性质得出BE=AC即可.
(2)根据全等三角形的性质得出BE=AC即可.
解答:(1)解:∵△ACB是等腰直角三角形,
∴AC=BC,∠CAB=∠CBA=45°
∵△ABD和△DEC是等边三角形,
∴AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°
∴∠DAC=60°-45°=15°,∠DBC=15°,∠EDB=∠CDA=60°-∠BCD,
在△ADC和△BDE中
∴△ADC≌△BDE,
∴BE=AC=BC,∠EBD=∠CAD=15°,
∴∠BCE=∠BEC=
(180°-15°-15°)=75°;
(2)证明:∵△ADC≌△BDE,
∴BE=AC.
∴AC=BC,∠CAB=∠CBA=45°
∵△ABD和△DEC是等边三角形,
∴AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°
∴∠DAC=60°-45°=15°,∠DBC=15°,∠EDB=∠CDA=60°-∠BCD,
在△ADC和△BDE中
|
∴△ADC≌△BDE,
∴BE=AC=BC,∠EBD=∠CAD=15°,
∴∠BCE=∠BEC=
| 1 |
| 2 |
(2)证明:∵△ADC≌△BDE,
∴BE=AC.
点评:本题考查了等腰直角三角形的性质,等边三角形的性质,全等三角形的性质和判定的应用,解此题的关键是求出△ADC≌△BDE.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a2•a3=a6 |
| B、a4÷a=a3 |
| C、(-a2b)3=-a2b3 |
| D、(-b4)2=b8 |
 如图,小正方形的边长均为1的正方形网格中,O的圆心在格点上,求∠AED的余弦值.
如图,小正方形的边长均为1的正方形网格中,O的圆心在格点上,求∠AED的余弦值. 如图:点D在△ABC的边AB上,连接 CD,∠1=∠B,AD=4,AC=6,
如图:点D在△ABC的边AB上,连接 CD,∠1=∠B,AD=4,AC=6,