题目内容
莉莉的爸爸是一名装修工人,他用同样大小的灰、白两种正方形地砖铺设客厅的底面,设的方法是:第一层只有3块白色地砖,第二层在第一层外围一圈灰色地砖,第三层是在第二层外围一圈白色地砖…如图所示.
(1)第四层共有多少块正方形的地砖?是白色的还是灰色的?
(2)第n(n>1)层共有多少块正方形的地砖?
(3)莉莉的爸爸铺设万第8层时,总共用去了多少块正方形的地砖?
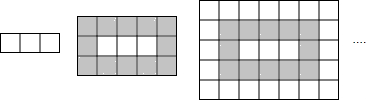
(1)第四层共有多少块正方形的地砖?是白色的还是灰色的?
(2)第n(n>1)层共有多少块正方形的地砖?
(3)莉莉的爸爸铺设万第8层时,总共用去了多少块正方形的地砖?

考点:规律型:图形的变化类
专题:
分析:(1)由图形可知单数层是白色瓷块,双数层是灰色地砖;第一层中白色瓷块有1×3块,第二层中灰色地砖有3×5-1×3块,第三层中白色瓷块有5×7-3×5块,…,可知第4层的地砖的块数及颜色;
(2)由(1)可知第n层的地砖有2n(2n-1)-(2n-2)(2n-3)=8n-6.
(3)第n个图形中地砖的数量=(2n-1)(2n+1).
(2)由(1)可知第n层的地砖有2n(2n-1)-(2n-2)(2n-3)=8n-6.
(3)第n个图形中地砖的数量=(2n-1)(2n+1).
解答:解:(1)第4层是偶数层,地砖是灰色的,地砖的块数是7×9-5×7=28块;
(2)第n层的地砖有(2n+1)(2n-1)-(2n-3)(2n-1)=8n-4;
(3)第n个图形中地砖的数量=(2n-1)(2n+1),当n=8时,地砖的数量=16×17=272块正方形的地砖.
(2)第n层的地砖有(2n+1)(2n-1)-(2n-3)(2n-1)=8n-4;
(3)第n个图形中地砖的数量=(2n-1)(2n+1),当n=8时,地砖的数量=16×17=272块正方形的地砖.
点评:考查了规律型:图形的变化,此类题中要注意能够正确发现规律:即第n个图案有地砖(2n-1)(2n+1)块.

练习册系列答案
相关题目
如图图形是数轴的是( )
A、 |
B、 |
C、 |
D、 |
下列计算正确的是( )
| A、a2•a3=a6 |
| B、a4÷a=a3 |
| C、(-a2b)3=-a2b3 |
| D、(-b4)2=b8 |
下列式子是因式分解的是( )
| A、a(a-b-1)=a2+ab-a | ||
| B、a2-a-3=a(a-1)-3 | ||
| C、-4a2+9b2=-(2a+3b)(2a-3b) | ||
D、2x+1=x(2+
|
 如图,AB是半圆的直径,BD是半圆的切线,C是半圆上任意一点,过C作BD的垂线,垂足为D,求证:AC是ED和AB的比例中项.
如图,AB是半圆的直径,BD是半圆的切线,C是半圆上任意一点,过C作BD的垂线,垂足为D,求证:AC是ED和AB的比例中项. 如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC=
如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC= 已知,如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,BE、DF分别交AD、BC于点E、F,求证:BE∥DF.
已知,如图,在平行四边形ABCD中,BE、DF分别平分∠ABC、∠ADC,BE、DF分别交AD、BC于点E、F,求证:BE∥DF.