题目内容
3.如果关于x的一元二次方程x2-4x+3m=0有两个不相等的实数根,则m的取值范围是m<$\frac{4}{3}$.分析 根据题意一元二次方程有两不相等实根,则有△=b2-4ac=16-12m>0,然后解得m的取值范围.
解答 解:∵关于x的一元二次方程x2-4x+3m=0有两个不相等的实数根,
∴△>0,即△=16-12m>0,
∴m<$\frac{4}{3}$,
故答案为:m<$\frac{4}{3}$.
点评 本题主要考查了利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
11.下列说法正确的是( )
| A. | 顺次连接对角线相等的四边形各边中点得到的四边形是矩形 | |
| B. | 顺次连接对角线互相垂直的四边形各边中点得到的四边形是菱形 | |
| C. | 顺次连接矩形各边中点得到的四边形是正方形 | |
| D. | 顺次连接菱形各边中点得到的四边形是矩形 |
15.下列计算错误的是( )
| A. | -a2•(-a)2=-a4 | B. | (-a)2•(-a)4=a6 | C. | (-a3)•(-a)2=a5 | D. | (-a)•(-a)2=-a3 |

 如图所示,已知AB∥CD,BE平分∠ABF,DE平分∠CDG,∠BGD=50°,∠BED=60°,求∠ABF的度数.
如图所示,已知AB∥CD,BE平分∠ABF,DE平分∠CDG,∠BGD=50°,∠BED=60°,求∠ABF的度数.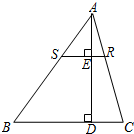 如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=$\frac{1}{3}$BC时,则DE=$\frac{2}{3}$h.
如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=$\frac{1}{3}$BC时,则DE=$\frac{2}{3}$h. 如图,点O在直线AB上,OE⊥AB,垂足为点O,OC⊥OD.若∠DOE=32°,请你求出∠EOC,∠BOD的度数,并说明理由.
如图,点O在直线AB上,OE⊥AB,垂足为点O,OC⊥OD.若∠DOE=32°,请你求出∠EOC,∠BOD的度数,并说明理由.