题目内容
18.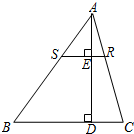 如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=$\frac{1}{3}$BC时,则DE=$\frac{2}{3}$h.
如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=$\frac{1}{3}$BC时,则DE=$\frac{2}{3}$h.
分析 根据AD⊥BC,SR⊥AD可得出SR∥BC,故△ASR∽△ABC,再由相似三角形的性质可得出AE的长,进而可得出结论.
解答 解:∵AD⊥BC,SR⊥AD,SR=$\frac{1}{3}$BC,AD=h,
∴SR∥BC,
∴△ASR∽△ABC,
∴$\frac{SR}{BC}$=$\frac{AE}{AD}$,即$\frac{1}{3}$=$\frac{AE}{h}$,解得AE=$\frac{1}{3}$h,
∴DE=AD-AE=h-$\frac{1}{3}$h=$\frac{2}{3}$h.
故答案为:$\frac{2}{3}$h.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形对应高的比等于相似比是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,已知点A是双曲线y=$\frac{4}{x}$第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-12.
如图,已知点A是双曲线y=$\frac{4}{x}$第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-12. 如图所示,AC⊥BD,O为垂足,试说明AB2+CD2=AD2+BC2.
如图所示,AC⊥BD,O为垂足,试说明AB2+CD2=AD2+BC2.