题目内容
11.设M(p,q)为二次函数y=mx2-(m+1)x+1图象上的一个动点,当-3<p<0时,点M关于x轴的对称点都在直线y=-x-1的下方,求m的取值范围.分析 根据题意可知,存在两种情况,m>0或m<0,然后根据题目中的信息分别讨论m的求值范围,本题得以解决.
解答 解:∵y=mx2-(m+1)x+1=(mx-1)(x-1),
∴y=0时,${x}_{1}=\frac{1}{m},{x}_{2}=1$,
∵点M关于x轴的对称点都在直线y=-x-1的下方,M(p,q)为二次函数y=mx2-(m+1)x+1图象上的一个动点,
当m>0,-3<p<0时,-[mp2-(m+1)p+1]<-p-1,
解得,m>$\frac{2}{p-1}$,
∵m>0,-3<p<0,则$\frac{2}{p-1}<0$,
∴m>0;
当m<0,-3<p<0时,-[mp2-(m+1)p+1]<-p-1,
解得,m$<\frac{2}{p-1}$,
∵m<0,-3<p<0时,则$\frac{2}{p-1}<0$,
∴m<$\frac{2}{p-2}$;
由上可得,m的取值范围是m>0或m<$\frac{2}{p-2}$.
点评 本题考查二次函数的性质、一次函数的性质,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.如果一次函数y=kx-b的图象经过第一、二、三象限,那么k的取值范围是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
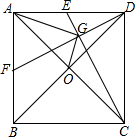 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D. 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.