题目内容
20. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.(1)求点A的坐标;
(2)若BC=4,
①求抛物线的解析式;
②将抛物线在C,D之间的部分记为图象G(包含C,D两点).若过点A的直线y=kx+b(k≠0)与图象G有两个交点,结合函数的图象,求k的取值范围.
分析 (1)把一般式配成顶点式即可得到A点坐标;
(2)已知BC=4,由(1)可知抛物线对称轴为x=1,所以可知B点坐标,将其代入抛物线方程可求得m的值,于是得到抛物线解析式;
②由m=1即可得到B(-1,0),C(3,0),再求出D(0,-3),画出抛物线,通过画图可得当k>0时,直线y=kx+b过A、C时,k最大;当k<0,直线y=kx+b过A、D时,k最大,然后分别求出两直线解析式即可得到k的范围.
解答 解:(1)y=mx2-2mx+m-4=m(x-1)2-4,
所以抛物线的顶点A的坐标为(1,-4);
(2)①∵BC=4,抛物线的对称轴为x=1,点B在点C左侧,
∴点B坐标为(-1,0),点C坐标为(3,0),
将B(-1,0)代入y=m(x-1)2-4,得:0=4m-4,解得m=1
所以抛物线的解析式为y=(x-1)2-4=x2-2x-3;
②B(-1,0),C(3,0),
当x=0时,y=x2-2x-3=-3,则D(0,-3),如图,
当直线y=kx+b过A、C时,直线解析式为y=2x-6;
当直线y=kx+b过A、D时,直线解析式为y=-x-3,
所以若过点A的直线y=kx+b(k≠0)与图象G有两个交点,k的取值范围为0<k≤2或-1≤k<0.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质和一次函数图象的性质.

练习册系列答案
相关题目
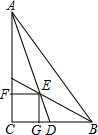 如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )
如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )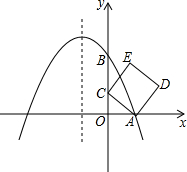 如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.
如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.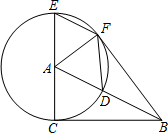 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.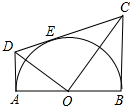 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )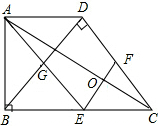 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.