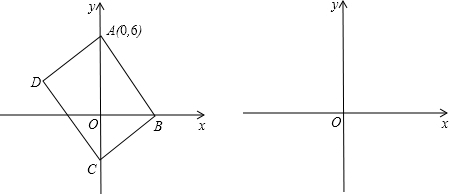题目内容
1. 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
分析 因为直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解,所以,直线l与m的交点的坐标为方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解.
解答 解:∵直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解,
∴直线m的解析式为x+y=4,直线n的解析式为x-3y=0,
∴直线l与m的交点的坐标为方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解;
∵从图中观察得知,l与m的交点M的坐标为(1,1),
∴方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
故答案为(1,1),$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
点评 本题考查了一次函数和二元一次方程组的关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
相关题目
13. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积为( )| A. | 2$\sqrt{3}$ | B. | 3π-2$\sqrt{3}$ | C. | 3π-4$\sqrt{3}$ | D. | 3π |
16.如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )
| A. | S和C | B. | S和a | C. | C和a | D. | S,C,a |
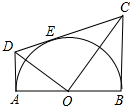 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )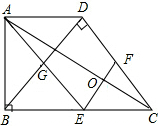 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.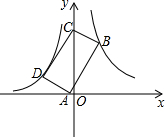 如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.
如图,点B(3,6)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{8}{x}$(x<0)上,点A和点C分别在x轴和y轴上,且四边形ABCD是矩形,AB=2BC.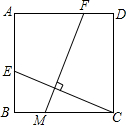 已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM.
已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM.