题目内容
8.以△ABC的边AB、AC为直角边分别向外作等腰直角△ABD和△ACE,M是BC的中点,N是DE的中点,连接AM、AN.(1)如图1,当∠BAC=90°时,其他条件不变,猜想线段BM与AN之间的数量关系,并证明你的猜想;
(2)如图2,当∠BAC≠90°时,其他条件不变,那么(1)中猜想的结论是否成立,如果成立,请给出证明;如果不成立,请说明理由.
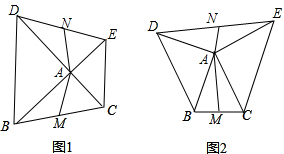
分析 (1)先由SAS证明△ABC≌△ADE,得出BC=DE,再由已知条件得出BM=CM=$\frac{1}{2}$BC,AN=$\frac{1}{2}$DE=$\frac{1}{2}$BC,即可得出结论;
(2)延长AN至F,使NF=AN,连接DF,先证明△ANE≌△FND,得出DF=AE=AC,∠F=NAE,证出DF∥AE,再证出∠FDA=∠BAC,由SAS证明△ABC≌△DAF,得出BC=AF,即可得出结论.
解答 解:(1)BM=AN;证明如下:
∵△ABD和△ACE是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°,
又∵∠BAC=90°,
∴∠EAD=90°.
∴∠BAC=∠DAE,
在△ABC和△ADE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAC=∠DAE}&{\;}\\{AC=AE}&{\;}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴BC=DE,
∵M是BC的中点,N是DE的中点,
∴BM=CM=$\frac{1}{2}$BC,AN=$\frac{1}{2}$DE=$\frac{1}{2}$BC,
∴BM=AN;
(2)成立;证明如下:如图2所示: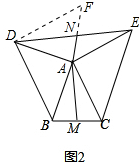
延长AN至F,使NF=AN,连接DF,
∵N是DE的中点,
∴DN=NE,
在△ANE和△FND中,$\left\{\begin{array}{l}{NE=DN}&{\;}\\{∠ANE=∠FND}&{\;}\\{AN=NF}&{\;}\end{array}\right.$,
∴△ANE≌△FND(SAS),
∴DF=AE=AC,∠F=NAE,
∴DF∥AE,
∴∠FDA+∠DAE=180°,
∵∠BAC+∠DAE=360°-∠BAD-∠CAE=180°,
∴∠FDA=∠BAC,
在△ABC和△DAF中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAC=∠FDA}&{\;}\\{AC=DF}&{\;}\end{array}\right.$,
∴△ABC≌△DAF(SAS),
∴BC=AF,
∵BM=CM=$\frac{1}{2}$BC,AN=$\frac{1}{2}$AF=$\frac{1}{2}$BC,
∴BM=AN.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质以及平行线的判定;证明三角形全等是解决问题的关键.

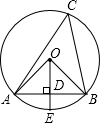 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )| A. | ∠ACB=∠AOE | B. | AD=BD | C. | S△AOB=$\frac{1}{2}$S△ABC | D. | AE=BE |
初次见面,通常以握手示礼,适当的握手时间与力度,会让人有股舒服亲切的感受.9月1日开学时,老师为了让全班新同学互相认识,请班上41位同学彼此握手为礼,并同时彼此介绍自己.在一阵喧哗后,同学完成工作.老师提出一个问题:“谁知道,刚才全班同学总共握手几次?”小聪同学举手抢答说820次,他说的对不对?
探索研究
其实要解决握手问题,可以作以下的分析:假若两点代表两个人,连接两点的线段数目,就表示握手的次数. 我们可以作一个由点和线段组成的图来分析一下
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
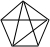 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+(n+1) |
解决问题
班上41位同学彼此握手为礼,他们共握手多少次?小聪同学说的对不对?
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点?请你完成下表:
| 图标 | 直线条数 | 交点个数 |
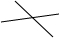 | 2 | 1 |
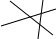 | 3 | 3=1+2 |
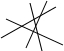 | 4 | |
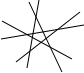 | 5 | |
| … | … | … |
| … | n |
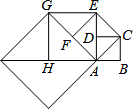 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2013=21006.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a2013=21006.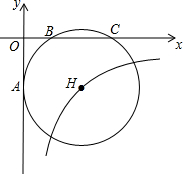 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.