题目内容
11.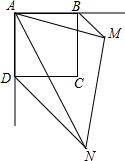 已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.(1)求证:△ABM∽△NDA;
(2)联结BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
分析 (1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;
(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°-∠DAN,
∴△ABM∽△NDA;
(2)解:∵四边形BMND为矩形,
∴BM=DN,
∵△ABM∽△NDA,
∴$\frac{AB}{DN}$=$\frac{BM}{AD}$,
∴BM2=AB2,
∴BM=AB,
∴∠BAM=∠BMA=$\frac{180°-∠ABM}{2}$=22.5°.
点评 此题考查了相似三角形的判定与性质、正方形的性质以及矩形的性质.注意能证得当四边形BMND为矩形时,△ABM是等腰三角形是难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.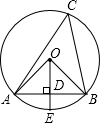 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )| A. | ∠ACB=∠AOE | B. | AD=BD | C. | S△AOB=$\frac{1}{2}$S△ABC | D. | AE=BE |
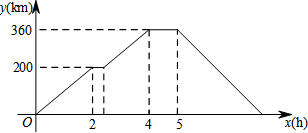
 如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)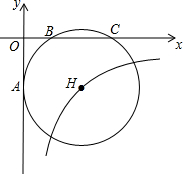 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则k=-8$\sqrt{3}$.