题目内容
20.已知直线y=kx+b经过A(1,3),B(-1,-1)两点.(1)求k、b的值;
(2)求直线与x轴的交点坐标;
(3)求不等式kx+b>0的解集.
分析 (1)利用待定系数法求一次函数解析式,从而得到k和b的值;
(2)求函数值为0时的函数值即可得到直线与x轴的交点坐标;
(3)利用一次函数与一元一次不等式的关系写出函数图象在x轴上方所对应的自变量的范围即可.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{k+b=3}\\{-k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=1}\end{array}\right.$;
(2)一次函数解析式为y=2x+1,
当y=0时,2x+1=0,解得x=-$\frac{1}{2}$,
所以直线与x轴的交点坐标为(-$\frac{1}{2}$,0);
(2)当x>-$\frac{1}{2}$时,y>0,
所以不等式kx+b>0的解集为x>-$\frac{1}{2}$.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
10. 如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
 如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
8. 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )| A. | 70° | B. | 40° | C. | 35° | D. | 30° |
 在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.
在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.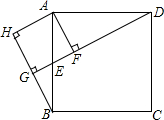 如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.
如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.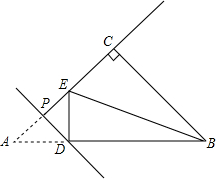 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.