题目内容
7.下列方程中,没有实数根的是( )| A. | x2-2x=0 | B. | x2-2x-1=0 | C. | x2-2x+1=0 | D. | x2-2x+2=0 |
分析 分别计算各方程的根的判别式的值,然后根据判别式的意义判定方程根的情况即可.
解答 解:A、△=(-2)2-4×1×0=4>0,方程有两个不相等的实数根,所以A选项错误;
B、△=(-2)2-4×1×(-1)=8>0,方程有两个不相等的实数根,所以B选项错误;
C、△=(-2)2-4×1×1=0,方程有两个相等的实数根,所以C选项错误;
D、△=(-2)2-4×1×2=-4<0,方程没有实数根,所以D选项正确.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
2.-2的倒数是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12.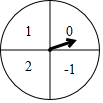 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
12.某房地产开发公司计划建A、B两种户型的住房共80套,A种户型每套成本和售价分别为90万元和102万元,B种户型每套成本和售价分别为60万元和70万元.设计划建A户型x套,所建户型全部售出后获得的总利润为W万元.
【思考】
(1)根据所给条件,完成下表:
(2)求W与x之间的函数解析式;
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
【思考】
(1)根据所给条件,完成下表:
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
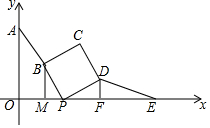 如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE. 2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.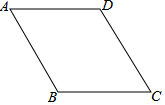 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
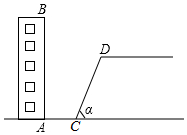 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)