题目内容
16.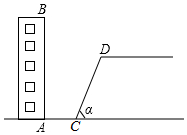 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
分析 假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,根据锐角三角函数的定义求出DE、CE、CE′的长,进而可得出结论.
解答  解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
解:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CD•sin60°=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$米,CE=CD•cos60°=12×$\frac{1}{2}$=6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6$\sqrt{3}$米.
∵∠D′CE′=39°,
∴CE′=$\frac{D′E′}{tan39°}$≈$\frac{6\sqrt{3}}{0.81}$≈12.8,
∴EE′=CE′-CE=12.8-6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
7.下列方程中,没有实数根的是( )
| A. | x2-2x=0 | B. | x2-2x-1=0 | C. | x2-2x+1=0 | D. | x2-2x+2=0 |
4.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为( )
| A. | 2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |
8.下列调查中,适合用全面调查方式的是( )
| A. | 了解我市上班族的收入情况 | |
| B. | 了解全市市民的身高情况 | |
| C. | 了解某班学生期末考数学科成绩情况 | |
| D. | 了解我市的空气污染情况 |
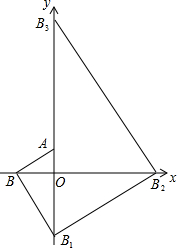 把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).
把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).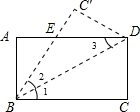 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=4,AB=2,则DE的长=2.5.
如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=4,AB=2,则DE的长=2.5.