题目内容
12.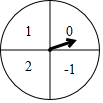 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两个数字都是正数的情况数,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有16种等可能的结果,两个数字都是正数的有4种情况,
∴两个数字都是正数的概率是:$\frac{4}{16}$=$\frac{1}{4}$.
故选:C.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件,解题时注意:概率=所求情况数与总情况数之比.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,先从中摸出一个小球,再从余下的球中摸出一个小球,第二次摸到小球的编号大于第一次编号的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
3.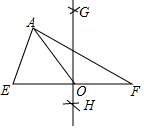 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )| A. | AO平分∠EAF | B. | AO垂直平分EF | C. | GH垂直平分EF | D. | GH平分AF |
7.下列方程中,没有实数根的是( )
| A. | x2-2x=0 | B. | x2-2x-1=0 | C. | x2-2x+1=0 | D. | x2-2x+2=0 |
4.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为( )
| A. | 2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |
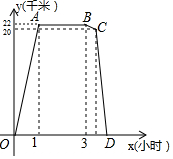 某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.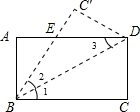 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=4,AB=2,则DE的长=2.5.
如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=4,AB=2,则DE的长=2.5. 2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
2016年1月21日01:13:13,青海海北州门源县发生6.4级地震.接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: