题目内容
15.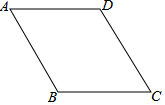 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
分析 分三种情形讨论①若以边BC为底.②若以边PB为底.③若以边PC为底.分别求出PD的最小值,即可判断.
解答 解:连接BD,在菱形ABCD中,
∵∠ABC=120°,AB=BC=AD=CD=10,
∴∠A=∠C=60°,
∴△ABD,△BCD都是等边三角形,
①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”,即当点P与点D重合时,PA最小,最小值PA=10;
②若以边PB为底,∠PCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧BD(除点B外)上的所有点都满足△PBC是等腰三角形,当点P在AC上时,AP最小,最小值为10$\sqrt{3}$-10;
③若以边PC为底,∠PBC为顶角,以点B为圆心,BC为半径作圆,则弧AC上的点A与点D均满足△PBC为等腰三角形,当点P与点A重合时,PA最小,显然不满足题意,故此种情况不存在;
综上所述,PD的最小值为10$\sqrt{3}$-10(cm);
故答案为:10$\sqrt{3}$-10.
点评 本题考查菱形的性质、等边三角形的性质、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
5.观察下列等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
| A. | 41 | B. | 45 | C. | 43 | D. | 44 |
6.随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
3.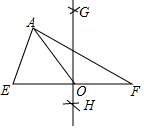 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
 如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )
如图,在△AEF中,尺规作图如下:分别以点E,点F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连接AO,则下列结论正确的是( )| A. | AO平分∠EAF | B. | AO垂直平分EF | C. | GH垂直平分EF | D. | GH平分AF |
7.下列方程中,没有实数根的是( )
| A. | x2-2x=0 | B. | x2-2x-1=0 | C. | x2-2x+1=0 | D. | x2-2x+2=0 |
4.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为( )
| A. | 2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | -2 |
 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )