题目内容
3．若a+b=1，求a3+b3+3ab的值．分析 先根据立方和公式得：a3+b3=（a+b）（a2-ab+b2），把a+b=1代入，再合并同类项后，是完全平方公式，代入即可得出结论．
解答 解：a3+b3+3ab，
=（a3+b3）+3ab，
=（a+b）（a2-ab+b2）+3ab，
=a2-ab+b2+3ab，
=a2+2ab+b2，
=（a+b）2，
=1．
点评 本题是因式分解的应用，考查了完全平方公式和立方和公式，将多项式化为a+b的式子是本题的关键．
练习册系列答案
百分学生作业本题练王系列答案
互动课堂系列答案
相关题目
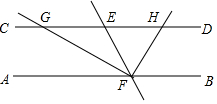如图，直线EF分别与直线AB，CD相交于点F，E，FG平分∠AFE交CD于点G，FH平分∠BFE交CD于点H，若∠GEF=7∠FGE，AB∥CD，那么∠HFB=70°．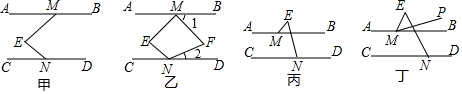
如图，在四边形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，AM⊥AD，交DC的延长线于点M，连接BM．
△ABC中，AB=AC，∠BAC=120°，AD⊥BC，且AB=6cm，求AD的长．