题目内容
18. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,AM⊥AD,交DC的延长线于点M,连接BM.
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,AM⊥AD,交DC的延长线于点M,连接BM.(1)求证:△DAC≌△MAB;
(2)求BD的长.
分析 (1)证出△ADM、△ABC是等腰直角三角形,得出AD=AM,AC=AB,∠DAM=∠CAB=90°,∠ADM=45°,证出∠DAC=∠MAB,由SAS证明△DAC≌△MAB即可;
(2)由全等三角形的性质得出AD=AM=4,CD=BM=3,∠AMB=∠ADM=45°,得出∠BMD=90°,由勾股定理求出DM=$\sqrt{A{D}^{2}+A{M}^{2}}$=4$\sqrt{2}$,在Rt△BDM中,由勾股定理求出BD即可.
解答 (1)证明:∵∠ABC=∠ACB=∠ADC=45°,AM⊥AD,
∴△ADM、△ABC是等腰直角三角形,
∴AD=AM,AC=AB,∠DAM=∠CAB=90°,∠ADM=45°,
∴∠DAC=∠MAB,
在△DAC和△MAB中,$\left\{\begin{array}{l}{AD=AM}&{\;}\\{∠DAC=∠MAB}&{\;}\\{AC=AB}&{\;}\end{array}\right.$,
∴△DAC≌△MAB(SAS);
(2)解:∵△DAC≌△MAB,
∴AD=AM=4,CD=BM=3,∠AMB=∠ADM=45°,
∴∠BMD=45°+45°=90°,
∵DM=$\sqrt{A{D}^{2}+A{M}^{2}}$=4$\sqrt{2}$,
∴在Rt△BDM中,BD=$\sqrt{D{M}^{2}+B{M}^{2}}$=$\sqrt{32+9}$=$\sqrt{41}$.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理;熟练掌握勾股定理,证明三角形全等是解决问题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.某文具店销售甲、乙两种品牌的学生书包,这两种书包的进价和售价如下表所示:
该文具店计划购进甲、乙两种品牌学生书包若干个,共需3700元,预计全部销售后可获利900元(利润=(售价-进价)×销售量).
(1)该文具店计划购进甲、乙两种品牌的学生书包各多少个?
(2)通过市场调研,该店决定在原计划的基础上,减少甲种品牌学生书包的购进数量,增加乙种品牌书包的购进数量,且乙种品牌书包增加的数量是甲种品牌学生书包减少数量的2倍,若设甲种品牌学生书包减少的数量z个,用于购进这两种品牌学生书包的总资金不超过4000元,求z的取值范围,并求当z取何值时利润最大?最大利润是多少?
| 甲 | 乙 | |
| 进价(元/个) | 80 | 70 |
| 售价(元/个) | 95 | 90 |
(1)该文具店计划购进甲、乙两种品牌的学生书包各多少个?
(2)通过市场调研,该店决定在原计划的基础上,减少甲种品牌学生书包的购进数量,增加乙种品牌书包的购进数量,且乙种品牌书包增加的数量是甲种品牌学生书包减少数量的2倍,若设甲种品牌学生书包减少的数量z个,用于购进这两种品牌学生书包的总资金不超过4000元,求z的取值范围,并求当z取何值时利润最大?最大利润是多少?
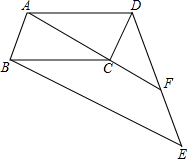 如图,四边形ABCD是平行四边形,连接AC并延长到点F,连接DF并延长到点E,使FE=DF,连接BE.
如图,四边形ABCD是平行四边形,连接AC并延长到点F,连接DF并延长到点E,使FE=DF,连接BE.