题目内容
已知抛物线y=-2x2+（k-1）x+k，若抛物线过原点，则k= ；若抛物线的顶点在y轴上，则k= ．
考点：二次函数的性质
专题：
分析：把原点（0，0）代入函数解析式求得相应的k的值即可；抛物线的顶点在y轴上，则该抛物线的对称轴是y轴．
解答：解：若抛物线过原点时：把（0，0）代入y=-2x2+（k-1）x+k，得
k=0；
若抛物线的顶点在y轴上时：
k-1=0，
解得 k=1．
故答案是：0；1．
k=0；
若抛物线的顶点在y轴上时：
k-1=0，
解得 k=1．
故答案是：0；1．
点评：本题主要考查了函数解析式与图象上的点之间的关系，点在图象上，则满足解析式；反之，满足解析式则在函数图象上．以及函数顶点在y轴上的条件，对称轴公式．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
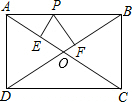在矩形ABCD中，P为AB上的动点，PE⊥AC于E，PF⊥BD于F，求证：PE+PF为定值．
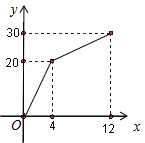有一个安装有进出水管的30升容器，水管每单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信息给出下列说法：