题目内容
已知x1、x2是方程x2-2（k-2）+（k2+3k+5）=0的两个实数根，求x12+x22．
考点：根与系数的关系,根的判别式
专题：
分析：设x1，x2是关于x的一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的两个实数根，则x1+x2=
，x1x2=
．根据x12+x22=（x1+x2）2-2x1x2即可求解．
| b |
| a |
| c |
| a |
解答：解：根据题意x1+x2=2（k-2），x1x2=k2+3k+5，
所以x12+x22=（x1+x2）2-2x1x2=4（k-2）2-4（k2+3k+5）=-28k-4．
所以x12+x22=（x1+x2）2-2x1x2=4（k-2）2-4（k2+3k+5）=-28k-4．
点评：本题考查了一元二次方程根与系数的关系和代数式变形，将根与系数的关系与代数式变形相结合是经常使用的一种解题方法．
练习册系列答案
相关题目
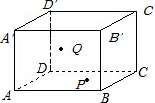如图是一个长方体形空水池，AB=10m，BC=5m，BB′=6m，在内壁ABB′A′的P处（点P到AB和BB′的距离都为1m）有一只壁虎，它想去吃在内壁CDD′C′上的Q处（点Q到CD和DD′的距离都为3m）的苍蝇，求它从点P爬到点Q的最短路径的长度．
在一张城市地图上，有学校、医院、图书馆三地，但被墨迹污染，图书馆的具体位置看不清，但知道图书馆在学校的东北方向，在医院的南偏西75°方向，你能确定图书馆的位置吗？
如图，已知D、E、F分别为等腰△ABC边BC、CA、AB上的点，如果AB=AC，∠FDE=∠B，BD=2，CD=3，CE=4，AE=1，那么AF的长为（ ）