题目内容
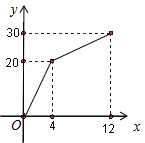 有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:
有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:①每分钟进水5升;
②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以下说法中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:一次函数的应用
专题:
分析:根据图象可以得到单独打开进水管4分钟注水20升,而同时打开放水管,8分钟内放进10升水,据此即可解答.
解答:解:①每分钟进水
=5升,则命题正确;
②当4≤x≤12时,y随x的增大而增大,因而容器中水量在增加,则命题错误;
③每分钟放水5-
=5-1.25=3.75升,
则放完水需要
=8(分钟),故命题正确;
④同时打开进水管和放水管,每分钟进水
=1.25升,则同时打开需要将容器灌满需要的时间是
=24(分钟),命题正确.
故选C.
| 20 |
| 4 |
②当4≤x≤12时,y随x的增大而增大,因而容器中水量在增加,则命题错误;
③每分钟放水5-
| 30-20 |
| 12-4 |
则放完水需要
| 30 |
| 3.75 |
④同时打开进水管和放水管,每分钟进水
| 30-20 |
| 12-4 |
| 30 |
| 1.25 |
故选C.
点评:本题考查了一次函数的图象,正确理解图象中表示的实际意义是关键.

练习册系列答案
相关题目
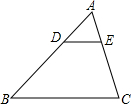 如图,△ABC中,DE∥BC,DE分别交边AB,AC于D,E两点,若AD:DB=1:3,则△ADE与四边形BDEC的面积比为
如图,△ABC中,DE∥BC,DE分别交边AB,AC于D,E两点,若AD:DB=1:3,则△ADE与四边形BDEC的面积比为