题目内容
△ABC是直角三角形,其中∠ACB=90°,AB=13,BC=12,AC=5,把△ABC绕A顺时针方向旋转90°后得到△AB1C1,此时∠BAB1=∠CAC1=90°,求线段BC在上述旋转过程中所扫过部分的周长、面积.(结果保留π)
考点:旋转的性质,弧长的计算,扇形面积的计算
专题:计算题
分析:画出几何图形,以点A为圆心,AC为半径的弧交AB于E,交AB1于F,根据旋转的性质得B1C1=BC=12,∠BAB1=∠CAC1=90°,△ABC≌△AB1C1,再利用弧长公式计算出弧CC1的长度为
π,弧BB1的长度为
π,所以线段BC在旋转过程中所扫过部分的周长=CB+弧BB1的长+B1C1+弧CC1的长=24+9π;由于△ABC≌△AB1C1,则∠BAC=∠B1AC1,所以S扇形CAE=S扇形C1AF,然后利用扇形面积公式和线段BC在旋转过程中所扫过部分的面积=S扇形BAB1-S扇形EAF进行计算.
| 5 |
| 2 |
| 13 |
| 2 |
解答:解: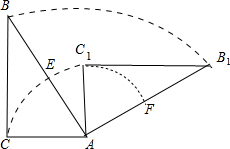 以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,
以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,
∵△ABC绕A顺时针方向旋转90°后得到△AB1C1,
∴B1C1=BC=12,∠BAB1=∠CAC1=90°,△ABC≌△AB1C1,
∴弧CC1的长度=
=
π,弧BB1的长度=
=
π,
∴线段BC在旋转过程中所扫过部分的周长=CB+弧BB1的长+B1C1+弧CC1的长
=12+
π+12+
π
=24+9π;
∵△ABC≌△AB1C1,
∴∠BAC=∠B1AC1,
∴S扇形CAE=S扇形C1AF,
∴线段BC在旋转过程中所扫过部分的面积=S扇形BAB1-S扇形EAF
=
-
=36π.
 以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,
以点A为圆心,AC为半径的弧交AB于E,交AB1于F,如图,∵△ABC绕A顺时针方向旋转90°后得到△AB1C1,
∴B1C1=BC=12,∠BAB1=∠CAC1=90°,△ABC≌△AB1C1,
∴弧CC1的长度=
| 90•π•5 |
| 180 |
| 5 |
| 2 |
| 90•π•13 |
| 180 |
| 13 |
| 2 |
∴线段BC在旋转过程中所扫过部分的周长=CB+弧BB1的长+B1C1+弧CC1的长
=12+
| 13 |
| 2 |
| 5 |
| 2 |
=24+9π;
∵△ABC≌△AB1C1,
∴∠BAC=∠B1AC1,
∴S扇形CAE=S扇形C1AF,
∴线段BC在旋转过程中所扫过部分的面积=S扇形BAB1-S扇形EAF
=
| 90•π•132 |
| 360 |
| 90•π•52 |
| 360 |
=36π.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了弧长公式和扇形的面积公式,会利用面积的和差计算不规则图形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
长沙地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:38,35,36,38,36,38,37,36,38,37(单位℃).则这组数据的中位数和众数分别是( )
| A、36,38 |
| B、37,38 |
| C、36.5,38 |
| D、37,36.5 |
 如图是6×8的正方形网格,△ABC的顶点都在格点上,M、N也在格点上.
如图是6×8的正方形网格,△ABC的顶点都在格点上,M、N也在格点上. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a>
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a>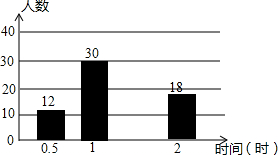 在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示: