Question

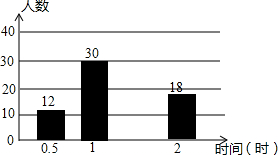在济南市开展的“美丽泉城，创卫我同行”活动中，某校倡议七年级学生利用双休日在各自社区参加义务劳动．为了解同学们劳动情况，学校随机调查了部分同学的劳动时间，并用得到的数据绘制成不完整的统计图表，如图所示：

劳动时间（时）	频数（人数）	频率
0.5	12	0.12
1	30	0.3
1.5	x	0.4
2	18	y
合计	m	1

（1）统计表中的x=

 

，y=

 

；
（2）被调查同学劳动时间的中位数是

 

时；
（3）请将频数分布直方图补充完整；
（4）求所有被调查同学的平均劳动时间．

Answer 1

考点：频数（率）分布直方图,频数（率）分布表,加权平均数,中位数

专题：

分析：（1）首先根据劳动时间是0.5小时的有12人，频率是0.12即可求得总数，然后根据频率的计算公式求得x、y的值；
（2）根据中位数的定义，即大小处于中间位置的数即可作出判断；
（3）根据（1）的结果即可完成；
（4）利用加权平均数公式即可求解．

解答：解：（1）调查的总人数是12÷0.12=100（人），
则x=100×0.4=40（人），
y=

18

100

=0.18；
（2）被调查同学劳动时间的中位数是1.5小时；
（3）
；
（4）所有被调查同学的平均劳动时间是：

12×0.5+30×1+40×1.5+18×2

100

=1.32（小时）．

点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．