题目内容
8.计算:(1)$\sqrt{12}-2tan{60°}+(-\frac{1}{3}{)^{-2}}-{2016^0}$
(2)$(x-2-\frac{12}{x+2})÷\frac{4-x}{x+2}$.
分析 (1)根据特殊角的三角函数值、负整数整数幂和零指数幂的意义计算;
(2)先把括号内通分和除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=2$\sqrt{3}$-2$\sqrt{3}$+9-1
=8;
(2)原式=$\frac{(x-2)(x+2)-12}{x+2}$•(-$\frac{x+2}{x-4}$)
=$\frac{(x+4)(x-4)}{x+2}$•(-$\frac{x+2}{x-4}$)
=-(x+4)
=-x-4.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了实数的运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 32=6 | C. | (-1)2015=-1 | D. | |-2|=-2 |
3.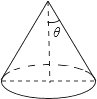 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
13.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.一个边长为a的正方形,若将其边长增加6cm,则新的正方形的面积增加( )
| A. | 36cm2 | B. | 12acm2 | C. | (36+12a)cm2 | D. | 以上都不对 |
 如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.
如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.