题目内容
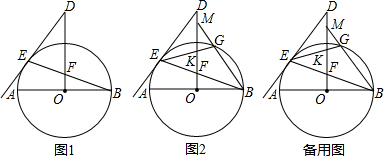
18. 如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.
如图,已知在四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,BD平分∠ABC,过点D作DF∥AB分别交AC、BC于点E、F.(1)求证:四边形ABFD是菱形;
(2)设AC⊥AB,求证:AC•OE=AB•EF.
分析 (1)根据已知条件得到四边形ABFD是平行四边形,由角平分线的定义得到∠ABD=∠DBC,根据平行线的性质得到∠ADB=∠CBD,等量代换得到∠ADB=∠ABD,证得AB=AD,即可得到结论;
(2)连接AF,OF,根据菱形的性质得到BD垂直平分AF,线段垂直平分线的性质得到AO=OF,由等腰三角形的性质得到∠ABD=∠FAC,推出△ABC∽△EOF,根据相似三角形的性质得到结论.
解答 证明:(1)∵AD∥BC,DF∥AB,
∴四边形ABFD是平行四边形,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴四边形ABFD是菱形;
(2)连接AF,OF,
∵AC⊥AB,∴∠BAC=90°,
∴∠CEF=∠BAC=90°,
∵四边形ABFD是菱形,
∴BD垂直平分AF,
∵AB⊥AC,
∴∠OAF+∠AOB=∠ABD+∠AOB=90°,
∴∠OAF=∠ABD,
∵BD垂直平分AF,
∴AO=OF,
∴∠OAF=∠OFA,
∴∠FOE=2∠FAO=2∠ABD=∠ABC,
∴△ABC∽△EOF,
∴$\frac{AC}{AB}=\frac{EF}{OE}$,
∴AC•OE=AB•EF.
点评 本题考查了菱形的判定和性质,平行线的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.已知α、β互余,且α比β大30°.则下列方程组中符合题意的是( )
| A. | $\left\{\begin{array}{l}α+β=180\\ α=β-30\end{array}\right.$ | B. | $\left\{\begin{array}{l}α+β=180\\ α=β+30\end{array}\right.$ | C. | $\left\{\begin{array}{l}α+β=90\\ α=β+30\end{array}\right.$ | D. | $\left\{\begin{array}{l}α+β=90\\ α=β-30\end{array}\right.$ |
13.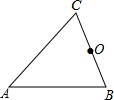 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
7.若a=b-3,则b-a的值是( )
| A. | -3 | B. | 3 | C. | 0 | D. | 6 |
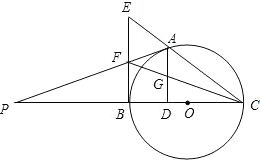 如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=$\frac{{\sqrt{2}}}{3}$;④OC=3$\sqrt{2}$,上述结论中正确的有①②④(填番号).