题目内容
16.我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;
(2)如图3,△ABC内接于⊙O,⊙O的半径为3$\sqrt{2}$,AB=6,∠BAC=30°,求AC的长;
(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求$\frac{AD}{CD}$的值.
分析 (1)由点C是弧BD的中点,根据弧与弦的关系,易得BC=CD,∠BAC=∠DAC,又由公共边AC,可证得:△ABC和△ACD是同族三角形;
(2)首先连接OA,OB,作点B作BE⊥AC于点E,易得△AOB是等腰直角三角形,继而求得答案;
(3)分别从当CD=CB时与当CD=AB时去分析求解即可求得答案.
解答 (1)证明:∵点C是弧BD的中点,即$\widehat{BC}$=$\widehat{CD}$,
∴BC=CD,∠BAC=∠DAC,
∵AC=AC,
∴△ABC和△ACD是同族三角形;
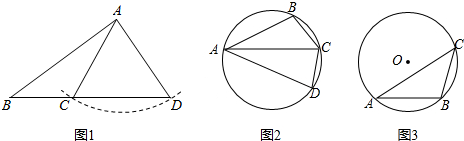
(2)解:如图1,连接OA,OB,作点B作BE⊥AC于点E,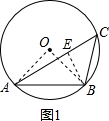 ∵OA=OB=3$\sqrt{2}$,AB=6,
∵OA=OB=3$\sqrt{2}$,AB=6,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,且∠AOB=90°,
∴∠C=$\frac{1}{2}$∠AOB=45°,
∵∠BAC=30°,
∴BE=$\frac{1}{2}$AB=3,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=3$\sqrt{3}$,
∵CE=BE=3,
∴AC=AE+CE=3$\sqrt{3}$+3;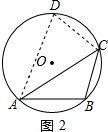 (3)解:∵∠B=180°-∠BAC-∠ACB=180°-30°-45°=105°,
(3)解:∵∠B=180°-∠BAC-∠ACB=180°-30°-45°=105°,
∴∠ADC=180°-∠B=75°,
如图2,当CD=CB时,∠DAC=∠BAC=30°,
∴∠ACD=75°,
∴AD=AC=3$\sqrt{3}$+3,CD=BC=$\sqrt{2}$BE=3$\sqrt{2}$,
∴$\frac{AD}{CD}$=$\frac{3\sqrt{3}+3}{3\sqrt{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$;
如图3,当CD=AB时,过点D作DF⊥AC,交AC于点F,
则∠DAC=∠ACB=45°,
∴∠ACD=180°-∠DAC-∠ADC=60°,
∴DF=CD•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴AD=$\sqrt{2}$DF=3$\sqrt{6}$,
∴$\frac{AD}{CD}$=$\frac{3\sqrt{6}}{6}$=$\frac{\sqrt{6}}{2}$.
综上所述:$\frac{AD}{CD}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$或$\frac{\sqrt{6}}{2}$.
点评 此题属于圆的综合题.考查了圆周角定理、弧与弦的关系、圆的内接四边形的性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

| A. | -3 | B. | 3 | C. | 0 | D. | 6 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
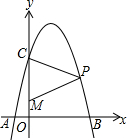 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).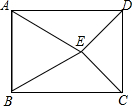 如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.
如图,在矩形ABCD内部,以AB为边作等边△ABE,且DE=CE,∠DEC=90°,求∠AED的度数.