题目内容
17.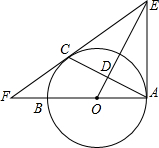 如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.
如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过C作⊙O的切线交OD的延长线于E,交AB的延长线于F,连EA.(1)求证:EA与⊙O相切;
(2)若CE=3,CF=2,求⊙O的半径.
分析 (1)连接OC,则∠OCE=90°,由D为中点可知EO⊥AC,则有CE=AE,可得∠ECA=∠EAC,且∠OCA=∠OAC,利用角的和差可求得∠EAO=90°,可知EA为切线;
(2)连接BC,可证明△FBC∽△FCA,再由切线长定理可知CE=AE,在Rt△AEF中可求得AF=8,再利用线段的比可求得AB的长,可得半径.
解答 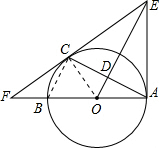 (1)证明:如图,连接OC,
(1)证明:如图,连接OC,
∵EF为切线,
∴∠OCE=90°,
∵D为AC中点,
∴OE⊥AC,
∴EC=EA,
∴∠ECA=∠EAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC+∠EAC=∠OCA+∠ECA=90°,
即∠EAO=90°,
∴EA为⊙O的切线;
(2)解:连接BC,
∵AB为直径,
∴∠BCA=90°,
∴∠CAB+∠CBA=90°,
∵EF为切线,
∴∠BCF+∠BCO=90°,且∠BCO=∠CBA,
∴∠BCF=∠CAF,
∴△BCF∽△CAF,
∴$\frac{CF}{AF}=\frac{BF}{CF}$,
由(1)知EA为⊙O切线,则EA=EC=3,EF=EC+FC=5,
在Rt△AEF中,可求得AF=4,
∴$\frac{2}{4}=\frac{BF}{2}$,解得BF=1,
∴AB=AF-BF=3,
∴⊙O的半径为$\frac{3}{2}$.
点评 本题主要考查切线的判定和性质及相似三角形的判定和性质,在(2)中利用相似求得BF的长是解题的关键.

练习册系列答案
相关题目
6.下列同类二次根式合并过程正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | a$\sqrt{c}$+b$\sqrt{c}$=a+b$\sqrt{c}$ | C. | 5$\sqrt{a}$+$\frac{1}{2}$$\sqrt{a}$=5+$\frac{1}{2}$$\sqrt{a}$ | D. | $\frac{1}{3}$$\sqrt{3a}$-$\frac{1}{4}$$\sqrt{3a}$=$\frac{1}{12}$$\sqrt{3a}$ |
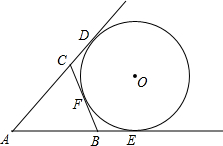 如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长.
如图,△ABC的周长等于16,圆O与BC相切于点F,AB、AC的延长线与圆分别相切于点E、D,求AE的长. 如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)