题目内容
14．计算：（1）a$\sqrt{\frac{3}{a}}$-$\sqrt{27a}$；
（2）（1+$\sqrt{a}$）2（1+$\sqrt{b}$）2（1-$\sqrt{a}$）2（1-$\sqrt{b}$）2．
分析 （1）直接化简二次根式进而合并即可；
（2）直接利用平方差公式化简计算求出答案．
解答 解：（1）a$\sqrt{\frac{3}{a}}$-$\sqrt{27a}$=$\sqrt{3a}$-3$\sqrt{3a}$=-2$\sqrt{3a}$；
（2）（1+$\sqrt{a}$）2（1+$\sqrt{b}$）2（1-$\sqrt{a}$）2（1-$\sqrt{b}$）2
=[（1+$\sqrt{a}$）（1-$\sqrt{a}$）]2[（1+$\sqrt{b}$）（1-$\sqrt{b}$）]2
=（1-a）2（1-b）2．
点评 此题主要考查了二次根式的混合运算，正确掌握乘法公式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
依据上述规律，
________．
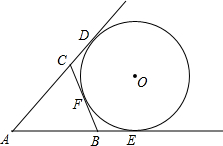如图，△ABC的周长等于16，圆O与BC相切于点F，AB、AC的延长线与圆分别相切于点E、D，求AE的长．
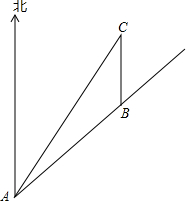如图，一条笔直的公路经过两个城镇A和B，为了改善居住条件，当地要建设一个新城镇C，已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处，且位于城镇B的正北方向，已知AB=4$\sqrt{2}$km，求新城镇C到公路的距离．（结果保留到0.1km，参考数据：$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41，$\sqrt{6}$≈2.45）
3．计算2$\sqrt{3}$+3$\sqrt{\frac{1}{3}}$-3$\sqrt{\frac{1}{27}}$的结果是（ ）
| A． | $\frac{8}{3}$$\sqrt{3}$ | B． | 8$\sqrt{\frac{1}{3}}$ | C． | 2$\sqrt{3}$ | D． | 2$\sqrt{3}$+$\frac{2}{3}$$\sqrt{\frac{1}{3}}$ |