题目内容
8.如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.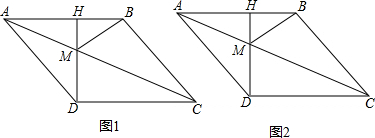
(1)求DM的长;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
分析 (1)方法一、由菱形的性质得到条件,判断出△AMH∽△CDM,由勾股定理计算出DH,即可;
方法二、先判断出△CDM≌△CBM,再用勾股定理即可求出DM,
(2)由△BCM≌△DCM计算出BM=DM,分两种情况计算即可;
(3)由菱形的性质判断出△ADM≌△ABM,再判断出△BMP是等腰三角形,即可.
解答 解:(1)在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BAC=∠DCA,
∵DH⊥AB,
∴∠AHD=∠CDH,
∴△AMH∽△CDM,
∴$\frac{HM}{DM}=\frac{AH}{CD}=\frac{3}{5}$,
∴$\frac{DH}{DM}=\frac{8}{5}$,
∵DH=4,
∴DM=$\frac{5}{2}$;
方法二、在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵AC是菱形ABCD的对角线,
∴∠ACD=∠ACB,CD=CB,
在△DCM和△BCM中,$\left\{\begin{array}{l}{CD=CB}\\{∠DCM=∠BCM}\\{CM=CM}\end{array}\right.$,
∴△DCM≌△BCM,
∴DM=BM,
在Rt△BHM中,BM=DM,HM=DH-DM=4-DM,BH=AB-AH=2,
根据勾股定理得,DM2-MH2=BH2,
即:DM2-(4-DM)2=4,
∴DM=$\frac{5}{2}$;
(2)在△BCM和△DCM中,
$\left\{\begin{array}{l}{CM=CN}\\{∠ACD=∠ACB}\\{CB=CD}\end{array}\right.$,
∴△BCM≌△DCM,
∴BM=DM=$\frac{5}{2}$,∠CDM=∠CBM=90°
①当P在AB之间时,S=$\frac{1}{2}$(5-2t)×$\frac{3}{2}$=-$\frac{3}{2}$t+$\frac{15}{4}$.
②当P在BC之间时,S=$\frac{1}{2}$(2t-5)×$\frac{5}{2}$=$\frac{5}{2}$t-$\frac{25}{4}$,
(3)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四边形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM,
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=2,
∴BP=2BH=4,
∵AB=5,
∴AP=1,
∴t=$\frac{AP}{2}$=$\frac{1}{2}$.
点评 此题是四边形综合题,主要考查了菱形的性质,和三角形全等的判定和性质,勾股定理得应用,∠MPB=∠ABM的判断是解本题的关键.

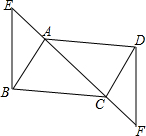 已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)
已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)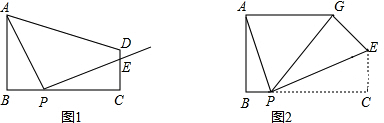
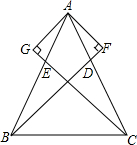 已知,如图,在△ABC中,AB=AC,BD、CE分别为AC、AB边上的中线,AF⊥BD于F,AG⊥CE于G.求证:AF=AG.
已知,如图,在△ABC中,AB=AC,BD、CE分别为AC、AB边上的中线,AF⊥BD于F,AG⊥CE于G.求证:AF=AG. 如图,△ABC中,点D、E在边BC上,且△ADE是等边三角形,∠BAC=120°,求证:DE2=BD•CE.
如图,△ABC中,点D、E在边BC上,且△ADE是等边三角形,∠BAC=120°,求证:DE2=BD•CE.