题目内容
1.(1)$2\sqrt{12}×\frac{{\sqrt{3}}}{4}÷\sqrt{2}$;(2)$\sqrt{45}$+$\sqrt{108}$+$\sqrt{1\frac{1}{3}}$-$\sqrt{125}$;
(3)($\frac{1}{2}$)-1×($\sqrt{3}$-$\sqrt{2}$)0+$\frac{4}{\sqrt{8}}$-|-$\sqrt{2}$|
(4)$({7+4\sqrt{3}})({7-4\sqrt{3}})-{({3\sqrt{5}-1})^2}$.
分析 (1)根据二次根式的乘除法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)根据零指数幂和负整数指数幂的意义运算;
(4)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=2×$\frac{1}{4}$×$\sqrt{12×3×\frac{1}{2}}$=$\frac{3\sqrt{2}}{2}$;
(2)原式=3$\sqrt{5}$+6$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$-5$\sqrt{5}$=$\frac{20\sqrt{3}}{3}$-2$\sqrt{5}$;
(3)原式=2×1+$\sqrt{2}$-$\sqrt{2}$=2;
(4)原式=49-48-(45-6$\sqrt{5}$+1)=1-46+6$\sqrt{5}$=6$\sqrt{5}$-45.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.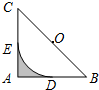 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )| A. | $1-\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{2}$ | D. | $2-\frac{π}{2}$ |
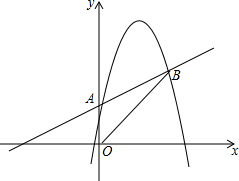 如图,已知抛物线y=-x2+bx+c经过A(0,1)、B(4,3)两点.
如图,已知抛物线y=-x2+bx+c经过A(0,1)、B(4,3)两点.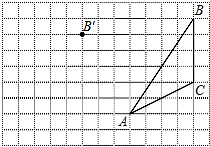 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.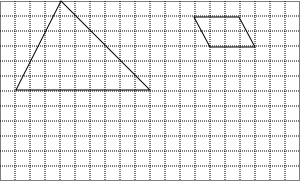 如图,每个小正方形的边长都是1
如图,每个小正方形的边长都是1