题目内容
9.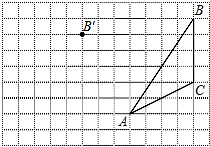 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是:平行且相等;
(4)求△A′B′C′的面积.
分析 (1)直接利用平移的性质得出各对应点位置进而得出答案;
(2)利用三角形中线的定义以及高线的定义分别得出答案;
(3)利用平移的性质得出对应点连线的关系;
(4)利用三角形面积求法得出答案.
解答  解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:中线CD和BC边上的高线AE即为所求;
(3)线段AA′与线段BB′的关系是:平行且相等;
故答案为:平行且相等;
(4)△A′B′C′的面积与△ABC的面积相等为:$\frac{1}{2}$×4×4=8.
点评 此题主要考查了平移变换以及三角形面积求法和三角形中线、高线的画法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
14.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 3:4:3:4 | B. | 5:2:2:5 | C. | 2:3:4:5 | D. | 3:3:4:4 |
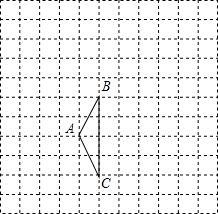 如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题: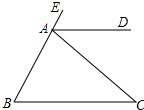 如图,E、A、B三点在同一直线上,AD平分∠EAC,AD∥BC,∠B=50°,则∠C的度数50°.
如图,E、A、B三点在同一直线上,AD平分∠EAC,AD∥BC,∠B=50°,则∠C的度数50°.