题目内容
11.设关于x的二次方程2mx2-(m+2)x-(m+1)=0有整数根,求整数m.分析 因式分解法求出方程的根,再根据整数根这个条件解决问题.
解答 解:∵2mx2-(m+2)x-(m+1)=0,
∴[mx-(m+1)](2x+1)=0,
∴x1=-$\frac{1}{2}$,x2=$\frac{m+1}{m}$=1+$\frac{1}{m}$,
由题意:m=±1,
经过检验m=±1都符合题意,
∴m=±1.
点评 本题考查根的判别式、因式分解法解方程,解题的关键是利用因式分解法解方程,把代数式化简为一个整式与一个分式的和(分式的分子不含有字母),属于中考常考题型.

练习册系列答案
相关题目
3.下列分解因式,正确的是( )
| A. | 4-x2+3x=(2-x)(2+x)+3x | B. | -x2+3x+4=-(x+4)(x-1) | ||
| C. | 4p3-6p2=2p(2p2-3p) | D. | (x-y)2-(y-x)=(y-x)(y-x-1) |
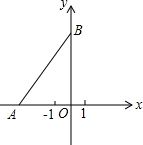 如图,在平面直角坐标系中,点A(-3b,0)为x轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程:3(b+1)=6.
如图,在平面直角坐标系中,点A(-3b,0)为x轴负半轴上一点,点B(0,4b)为y轴正半轴上一点,其中b满足方程:3(b+1)=6.