题目内容
11.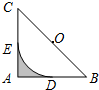 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )| A. | $1-\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{2}$ | D. | $2-\frac{π}{2}$ |
分析 连OD,OE,根据切线的性质得到OD⊥AB,OE⊥AC,则四边形OEAD为正方形,而AB=AC=2,O为BC的中点,则OD=OE=1,再根据正方形的面积公式和扇形的面积公式,利用S阴影部分=S正方形OEAD-S扇形OED,进行计算即可.
解答 解:连OD,OE,如图,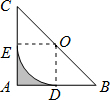
∴OD⊥AB,OE⊥AC,
∵∠A=90°,OE=OD,
∴四边形OEAD为正方形,
∵AB=AC=2,O为BC的中点,
∴OD=OE=$\frac{1}{2}$AC=1,
∴S阴影部分=S正方形OEAD-S扇形OED=1-$\frac{π}{4}$.
故选A.
点评 本题考查了扇形的面积公式:S=$\frac{nπ•{r}^{2}}{360}$,也考查了切线的性质定理以及正方形的性质.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
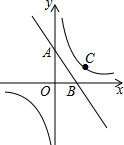 如图,A(0,4),B(3,0),C(4,2),且反比例函数图象经过点C.
如图,A(0,4),B(3,0),C(4,2),且反比例函数图象经过点C.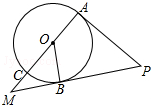 如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.求证:PB是⊙O的切线.
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.求证:PB是⊙O的切线.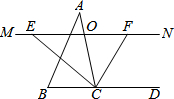 如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.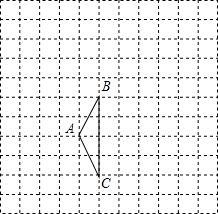 如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题: