题目内容
9. 如图,在平面直角坐标系xOy中,点A(-1,0),B(0,2),点C在第一象限,且满足∠ABC=135°,AC交y轴于点D,CD=3AD.
如图,在平面直角坐标系xOy中,点A(-1,0),B(0,2),点C在第一象限,且满足∠ABC=135°,AC交y轴于点D,CD=3AD.(1)求tan∠ABO的值;
(2)求点C的坐标.
分析 (1)在Rt△ABO中,根据三角函数的定义即刻得到结论;
(2)过O作OH⊥AB于H,得到AH=BH=$\frac{\sqrt{5}}{\sqrt{2}}$=$\frac{\sqrt{10}}{2}$,根据已知条件得到B,H,A,O四点共圆,连接OH,推出H在第二象限角平分线上,作HM⊥x轴于M,HN⊥y轴于N,根据全等三角形的性质得到AM=BN=$\frac{1}{2}$,求得直线HB的解析式,于是得到结论.
解答 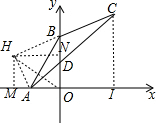 解:(1)在Rt△ABO中,AO=1,BO=2,
解:(1)在Rt△ABO中,AO=1,BO=2,
∴tan∠ABO=$\frac{AO}{BO}$=$\frac{1}{2}$;
(2)∵AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{5}$,
过O作OH⊥AB于H,
∵∠ABC=135°,
∴∠HBA=HAB=45°,
∴AH=BH=$\frac{\sqrt{5}}{\sqrt{2}}$=$\frac{\sqrt{10}}{2}$,
∵BH⊥AH,BO⊥AO,
∴B,H,A,O四点共圆,
连接OH,
∴∠BOH=∠BAH=45°,
∴H在第二象限角平分线上,
作HM⊥x轴于M,HN⊥y轴于N,
则四边形HMON是正方形,
∴HN=HN,
在Rt△AHM与Rt△BHN中,
$\left\{\begin{array}{l}{HM=HN}\\{AH=BH}\end{array}\right.$,
∴Rt△HAM≌Rt△HBN,
∴AM=BN,
∵OM=ON,
∴AM=BN=$\frac{1}{2}$,
∴H(-$\frac{3}{2}$,$\frac{3}{2}$),
∴直线BH的解析式为y=$\frac{1}{3}$x+2,
过C作CI⊥x轴于I,
∴OD∥CI,
∴$\frac{OA}{OI}=\frac{AD}{CD}$,
∴OI=3AO=3,
把x=3代入y=$\frac{1}{3}$x+2得y=3,
∴C点坐标为(3,3).
点评 本题考查了解直角三角形,正方形的判定和性质,求函数的解析式,全等三角形的判断和性质,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案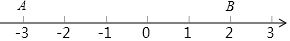 如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )
如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
| A. | x$>\frac{1}{2}$ | B. | x<-1 | C. | -1<x<$\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
| A. | 瓮中捉鳖 | B. | 刻舟求剑 | C. | 守株待兔 | D. | 水中捞月 |
 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m(克)的取值范围,在数轴上可表示为( )
如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m(克)的取值范围,在数轴上可表示为( )



 如图,在梯形ABCD中,AD∥BC,AB=CD,AC与BD相交于点E,∠ADB=60°,且BD:ED=3:1,BD=12,求梯形ABCD的周长.
如图,在梯形ABCD中,AD∥BC,AB=CD,AC与BD相交于点E,∠ADB=60°,且BD:ED=3:1,BD=12,求梯形ABCD的周长.