Question

汉口江滩有一个大型的圆形底面的喷水池，水池正中央装有一根高

13

16

米的水管，水管顶端装有一个喷水头，已知喷出的抛物线形水柱在与池中心的水平距离为3米处达到最高高度为

49

16

米，
（1）请建立适当的平面直角坐标系，使水管顶端的坐标为（0，

13

16

），水柱的最高点的坐标为（3，

49

16

），求此坐标系中抛物线对应的函数关系式（不要求写出自变量的取值范围）．
（2）如图，在水池底面上有一些同心圆轨道，每条轨道上安装了喷水龙头，相邻轨道之间的宽度为l米，最内轨道的半径为r米，其上每1.2米的弧长上装有一个喷水龙头，其他轨道上的喷水龙头个数与最内轨道上的个数相同．（1）中水柱落地处刚好在最外轨道上，求当r为多少时，水池中安装的喷水龙头的个数最多？

Answer 1

考点：二次函数的应用

专题：

分析：（1）根据题意确定抛物线的顶点坐标为（3，

49

16

），设抛物线解析式为y=a（x-3）²+

49

16

，根据水柱高为

13

16

米，将点（0，

13

16

）代入抛物线解析式求a即可；
（2）根据（1）中求出的抛物线解析式求水柱落地点离池中心的距离，根据池中安装水龙头的个数m=内圈装水龙头的个数×圈数，列出函数关系式，根据二次函数的性质求最大值．

解答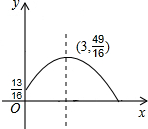：解：（1）如图，依题意建立平面直角坐标系，
∵点（1，3）为抛物形水柱的顶点，
∴设抛物线解析式为y=a（x-3）²+

49

16

，将点（0，

13

16

）代入，得

13

16

=a（0-3）²+

49

16

，
解得a=-

1

4

，
因此，抛物形水柱对应的函数关系式为：y=-

1

4

（x-3）²+

49

16

；

（2）当y=0时，-

1

4

（x-3）²+

49

16

=0，
解得x₁=-

1

2

，x₂=

13

2

，
根据实际，x=-

1

2

舍去，
所以，x=

13

2

，即水柱落地点离池中心

13

2

m，
设池中安装水龙头m个，依题意得
m=

2πr

1.2

•

6.5-r

1

，即m=

5

3

π（6.5r-r²）=-

5

3

π（r-

13

4

）²+

845

48

π，
所以当r=

13

4

时，池中安装的水龙头的个数最多．

点评：本题考查了二次函数的运用．关键是根据题意设抛物线解析式，根据条件求抛物线解析式，再列出池中安装水龙头个数的函数关系式．