题目内容
描述并说明：海宝在研究数学问题时发现了一个有趣的现象：
请根据海宝对现象的描述，用数学式子填空，并说明结论成立的理由．
如果 （其中a＞0，b＞0）．
那么 （结论）．
理由 ．
请根据海宝对现象的描述，用数学式子填空，并说明结论成立的理由．
如果
那么
理由
考点：分式的混合运算
专题：图表型
分析：根据题意列出关系式，猜想得到结论，利用分式的加减法则计算，再利用完全平方公式变形即可得证．
解答：解：如果
+
+2=ab（其中a＞0，b＞0），
那么a+b=ab；
理由：∵
+
+2=ab，
∴
=ab，
∴a2+b2+2ab=（ab）2，即（a+b）2=（ab）2，
则a+b=ab．
故答案为：
+
+2=ab；
a+b=ab；
∵
+
+2=ab，
∴
=ab，
∴a2+b2+2ab=（ab）2，即（a+b）2=（ab）2，
则a+b=ab．
| a |
| b |
| b |
| a |
那么a+b=ab；
理由：∵
| a |
| b |
| b |
| a |
∴
| a2+b2+2ab |
| ab |
∴a2+b2+2ab=（ab）2，即（a+b）2=（ab）2，
则a+b=ab．
故答案为：
| a |
| b |
| b |
| a |
a+b=ab；
∵
| a |
| b |
| b |
| a |
∴
| a2+b2+2ab |
| ab |
∴a2+b2+2ab=（ab）2，即（a+b）2=（ab）2，
则a+b=ab．
点评：此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
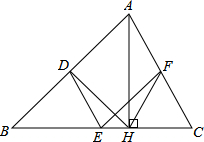如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．
今年“六一”儿童节当天，小兵一家三口自驾车去离家220千米的“儿童乐园”游玩，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．
如图，已知DE∥BC，BE平分∠ABNC，∠C=55°，∠ABC=70°．
如图，在平面直角坐标系，A（a，0），B（b，0），C（-1，2），且|2a+b+1|+（a+2b-4）2=0．
