题目内容
分解因式：
（1）-3x4+24x2-48；
（2）6a（x-1）2-2（1-x）2（a-4b）．
（1）-3x4+24x2-48；
（2）6a（x-1）2-2（1-x）2（a-4b）．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）首先提取公因式-3，进而利用平方差公式以及完全平方公式进行分解即可；
（2）首先提取公因式（x-1）2，进而合并同类项得出即可．
（2）首先提取公因式（x-1）2，进而合并同类项得出即可．
解答：解：（1）原式=-3（x4-8x2+16）
=-3（x2-4）2
=-3（x+2）2（x-2）2；
（2）原式=（x-1）2[6a-2（a-4b）]
=（x-1）2（4a+8b）
=4（x-1）2（a+2b）．
=-3（x2-4）2
=-3（x+2）2（x-2）2；
（2）原式=（x-1）2[6a-2（a-4b）]
=（x-1）2（4a+8b）
=4（x-1）2（a+2b）．
点评：此题主要考查了提取公因式法以及公式法分解因式，熟练掌握乘法公式是解题关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了10000人，并进行统一分析．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例的人数多22人．如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（ ）
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
不等式3-x＜1的解集是（ ）
| A、x＞2 | B、x＞-2 |
| C、x＜2 | D、x＜-2 |
函数y=
+3中，自变量x的取值范围是（ ）
| 1 | ||
|
| A、x＞5 | B、x≥-5 |
| C、x≤-5 | D、x＞-5 |
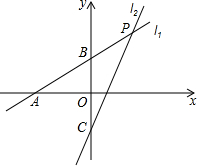如图，直线l1：y=k1+b1（k≠0）分别与x轴、y轴相交于点A（-5，0）和点B（0，2），直线l2：y=2x+b2 与直线l1相交于点P、与y轴相交于点C，已知点P的纵坐标为3．