题目内容
14.一次函数y=kx+b,当1<x<4时,-3<y<3,则这个函数的解析式为y=2x-5或y=-2x+5.分析 分类讨论:由于一次函数是递增或递减函数,所以当一次函数y=kx+b为增函数时,则x=1,y=-3;x=4,y=3,当一次函数y=kx+b为减函数时,则x=1,y=3;x=4,y=-3,然后把它们分别代入y=kx+b中得到方程组,再解两个方程组即可.
解答 解:①当一次函数经过点(1,-3)、(4,3)时,
有:$\left\{\begin{array}{l}{k+b=-3}\\{4k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-5}\end{array}\right.$,
则一次函数解析式为:y=2x-5;
②当一次函数经过(1,3)、(4,-3)时,
有:$\left\{\begin{array}{l}{k+b=3}\\{4k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=5}\end{array}\right.$,
则一次函数解析式为:y=-2x+5,
综上,该一次函数解析式为:y=2x-5或y=-2x+5,
故答案为:y=2x-5或y=-2x+5.
点评 本题考查了待定系数法求一次函数解析式:先设一次函数的解析式为y=kx+b,然后把一次函数图象上两点的坐标代入得到关于k、b的方程组,解方程组求出k、b的值,从而确定一次函数的解析式.也考查了分类讨论思想的运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.计算$\frac{\sqrt{5}a}{\sqrt{10a}}$得到的最后结果是( )
| A. | $\frac{\sqrt{a}}{\sqrt{2}}$ | B. | $\frac{\sqrt{2a}}{2}$ | C. | $\sqrt{\frac{a}{2}}$ | D. | $\sqrt{\frac{2a}{2}}$ |
4.为鼓励节约用水,高港区自来水公司推行阶梯式水价计费制,标准如下表:
已知王奶奶家今年5月份用了8吨水,共缴纳水费12元.
(1)请求出a的值;
(2)若小明家今年8月份共缴纳水费37元,请求出8月份小明家的用水量.
| 用水吨数 | 水费缴纳标准 |
| 每月用水不超过10吨 | 每吨a元收费 |
| 若每月用水超过10吨 | 超过部分每吨2元收费 |
(1)请求出a的值;
(2)若小明家今年8月份共缴纳水费37元,请求出8月份小明家的用水量.
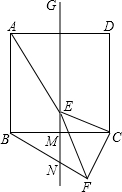 已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N
已知如图,正方形ABCD中,GM是其对称轴,E点是线段GM上的点,连接CE,以CE为直角边作等腰直角三角形CEF,∠ECF=90°,连接FB交直线GM于N △ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.
△ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.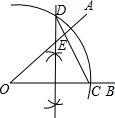 如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.
如图,∠AOB=40°,在射线OB上取点C,以O为圆心,OC长为半径作圆弧,交OC的垂直平分线于点D(点D在OC上方),连结CD交OA于点E,则∠AEC=100度.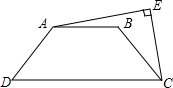 如图,在等腰梯形ABCD中,AB∥CD,AB=6,CD=14,∠AEC=90°,CE=CB,则AE2=84.
如图,在等腰梯形ABCD中,AB∥CD,AB=6,CD=14,∠AEC=90°,CE=CB,则AE2=84.