Question

4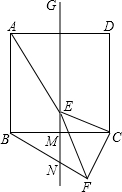．已知如图，正方形ABCD中，GM是其对称轴，E点是线段GM上的点，连接CE，以CE为直角边作等腰直角三角形CEF，∠ECF=90°，连接FB交直线GM于N
（1）求证：BF=AE；
（2）当∠AEG=30°时，求$\frac{BN}{BF}$的值．

Answer 1

分析 （1）连接DE，如图，由对称性可得AE=DE，要证BF=AE，只需证BF=DE，只需证△BCF≌△DCE即可；
（2）由∠AEG=30°可推出∠CBF=30°，运用三角函数可得到BN与BM的关系、AG与AE的关系、易得AG=BM，从而得到BN与AE的关系，再结合（1）中的结论BF=AE就可解决问题．

解答 解：（1）连接DE，如图．
∵四边形ABCD是正方形，
∴AD=CD=CB，∠BCD=90°．
∵∠ECF=90°，
∴∠BCD=∠ECF，
∴∠BCF=∠DCE．
在△BCF和△DCE中，
$\left\{\begin{array}{l}{CF=CE}\\{∠BCF=∠DCE}\\{CB=CD}\end{array}\right.$，
∴△BCF≌△DCE，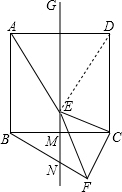
∴BF=DE．
∵GM是正方形ABCD的对称轴，
∴AE=DE，
∴BF=AE；

（2）∵GM是正方形ABCD的对称轴，
∴AG=$\frac{1}{2}$AD，BM=$\frac{1}{2}$BC，∠DEG=∠AEG，GM∥DC．
∵AD=BC，∴AG=BM．
∵∠AEG=30°，∴∠DEG=30°．
∵GM∥DC，∴∠CDE=∠DEG=30°．
∵△BCF≌△DCE，
∴∠CBF=∠CDE=30°．
在Rt△AGE中，sin∠AEG=$\frac{AG}{AE}$=$\frac{1}{2}$，
∴AE=2AG=2BM，
∴BF=AE=2BM．
在Rt△BMN中，cos∠CBF=$\frac{BM}{BN}$=$\frac{\sqrt{3}}{2}$，
∴BN=$\frac{2BM}{\sqrt{3}}$=$\frac{BF}{\sqrt{3}}$，
∴$\frac{BN}{BF}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$．

点评 本题主要考查了正方形的性质、全等三角形的判定与性质、轴对称图形的性质、三角函数等知识，证到△BCF≌△DCE是解决第（1）小题的关键，利用（1）中的结论BF=AE是解决第（2）小题的关键．