题目内容
3.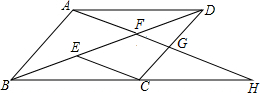 如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.
如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.(1)求证:四边形ABCD是平行四边形;
(2)延长AF,交边DC于点G,交边BC的延长线于点H,求证:AD•DC=BH•DG.
分析 (1)通过证明△ABF≌△CDE得到AB=CD,加上AB∥CD,则可判断四边形ABCD是平行四边形;
(2)根据平行四边形的性质得AD=BC,AD∥BC,再证明△CHG∽△DAG,利用相似比得到$\frac{CH}{AD}$=$\frac{CG}{DG}$,然后利用比例的性质和等线段代换即可得到结论.
解答 证明:(1)∵AB∥CD,
∴∠ABD=∠CDB,
∵AF∥EC,
∴∠AFB=∠CED,
∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{∠ABF=∠CDE}\\{BF=DE}\\{∠AFB=∠CED}\end{array}\right.$,
∴△ABF≌△CDE,
∴AB=CD,
而AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵CH∥AD,
∴△CHG∽△DAG,
∴$\frac{CH}{AD}$=$\frac{CG}{DG}$,
∴$\frac{CH+AD}{AD}$=$\frac{CG+DG}{DG}$,
即$\frac{BH}{AD}$=$\frac{CD}{DG}$,
∴AD•DC=BH•DG.
点评 本题考查了相似三角形的判定与性质:两个三角形相似对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.解决本题的关键是熟练掌握平行四边形的判定与性质.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
18.在“百度”搜索中输入“新版中小学生则”,相关结果约1660000个,这个数据可用科学记数法表示为( )
| A. | 166×104 | B. | 1.66×105 | C. | 1.66×106 | D. | 0.166×107 |
4.代数式2016-a2+2ab-b2的最大值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 不存在 |
 如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A. 如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$. 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.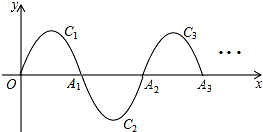 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.