题目内容
8. 如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.
分析 先证明∠AB′B=90°,再证明△ACE∽△ABB′,得到∠AEC=90°,利用面积法求出AE,再利用勾股定理求出EC即可.
解答 解:如图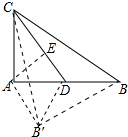 ,∵△CDB′是由□CDB翻折,
,∵△CDB′是由□CDB翻折,
∴∠BCD=∠DCB′,∠CBD=∠CDB′,AD=DB=DB′,
∴∠DBB′=∠DB′B,
∵2∠DCB+2∠CBD+2∠DBB′=180°,
∴∠DCB+∠CBD+∠DBB′=90°,
∵∠CDA=∠DCB+∠CBD,∠ACD+∠CDA=90°,
∴∠ABB′=∠ACE,
∵AD=DB=DB′=3,
∴∠AB′B=90°,
∵∠ACE=∠ABB′,∠CAE=∠BAB′,
∴△ACE∽△ABB′,
∴∠AEC=∠AB′B=90°,
在RT△AEC中,∵AC=4,AD=3,
∴CD=$\sqrt{A{C}^{2}+A{D}^{2}}$=5,
∵$\frac{1}{2}$AC•AD=$\frac{1}{2}$•CD•AE,
∴AE=$\frac{AC•AD}{CD}$=$\frac{12}{5}$,
在RT△ACE中,CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$.
故答案为$\frac{16}{5}$.
点评 本题考查翻折变换、相似三角形的判定和性质、勾股定理等知识,解题的关键是利用翻折不变性解决问题,学会利用相似三角形证明直角,属于中考常考题型.

练习册系列答案
相关题目
18.已知点A(-6,y1),B(-3,y2),C(3,y3)都在函数y=(x+2)2+m的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
11.下列命题中,真命题的是( )
| A. | 两个锐角的和为直角 | B. | 两个锐角的和为钝角 | ||
| C. | 两个锐角的和为锐角 | D. | 互余且非零度的两个角都是锐角 |
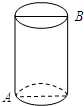 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).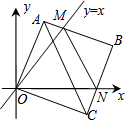 在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6.
在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为6. 如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.
如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.