题目内容
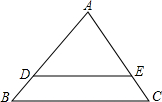 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质
专题:
分析:如图,证明△ADE∽△ABC,得到
=(
)2;证明
=
,求出
即可解决问题.
| S△ADE |
| S△ABC |
| DE |
| BC |
| S△ADE |
| S△ABC |
| 1 |
| 2 |
| DE |
| BC |
解答: 解:∵DE∥BC,
解:∵DE∥BC,
∴△ADE∽△ABC,
∴
=(
)2;
∵平行于BC的直线DE把△ABC分成的两部分面积相等,
∴
=
,
∴
=
,
故选D.
 解:∵DE∥BC,
解:∵DE∥BC,∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| DE |
| BC |
∵平行于BC的直线DE把△ABC分成的两部分面积相等,
∴
| S△ADE |
| S△ABC |
| 1 |
| 2 |
∴
| DE |
| BC |
| ||
| 2 |
故选D.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是牢固掌握相似三角形的判定及其性质.

练习册系列答案
相关题目
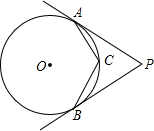 如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )
如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )| A、110° | B、115° |
| C、120° | D、125° |
 已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长.
已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长. 如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为
如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为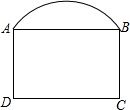 如图,工厂大门由弧线AB和矩形ABCD组成,
如图,工厂大门由弧线AB和矩形ABCD组成,
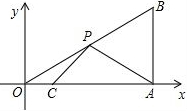 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为 “宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):
“宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60): 如图,点O在∠APB的平分线上,圆O与PA相切于点C.
如图,点O在∠APB的平分线上,圆O与PA相切于点C.