题目内容
 “宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):
“宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):(1)求每天销售量y(件)与售价x(元/件)之间的函数表达式;
(2)若该商品每天的利润为w(元),试确定w(元)与售价x(元/件)的函数表达式,并求售价x为多少时,每天的利润w最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)分别利用当20≤x≤40时,设y=ax+b,当40<x≤60时,设y=mx+n,利用待定系数法求一次函数解析式即可;
(2)利用(1)中所求进而得出w(元)与售价x(元/件)的函数表达式,进而求出函数最值.
(2)利用(1)中所求进而得出w(元)与售价x(元/件)的函数表达式,进而求出函数最值.
解答:解:(1)分两种情况:当20≤x≤40时,设y=ax+b,
根据题意,得
,
解得
,
故y=x+20;
当40<x≤60时,设y=mx+n,
根据题意,得
,
解得
,故
y=-2x+140;
故每天销售量y(件)与售价x(元/件)之间的函数表达式是:
y=
.
(2)w=
,
当20≤x≤40时,w=x2-400,
由于1>0抛物线开口向上,且x>0时w随x的增大而增大,又20≤x≤40,
因此当x=40时,w最大值=402-400=1200;
当40<x≤60时,w=-2x2+180x-2800=-2(x-45)2+1250,
由于-2<0,抛物线开口向下,又40<x≤60,
所以当x=45时,w最大值=1250.
综上所述,当当x=45时,w最大值=1250.
根据题意,得
|
解得
|
故y=x+20;
当40<x≤60时,设y=mx+n,
根据题意,得
|
解得
|
y=-2x+140;
故每天销售量y(件)与售价x(元/件)之间的函数表达式是:
y=
|
(2)w=
|
当20≤x≤40时,w=x2-400,
由于1>0抛物线开口向上,且x>0时w随x的增大而增大,又20≤x≤40,
因此当x=40时,w最大值=402-400=1200;
当40<x≤60时,w=-2x2+180x-2800=-2(x-45)2+1250,
由于-2<0,抛物线开口向下,又40<x≤60,
所以当x=45时,w最大值=1250.
综上所述,当当x=45时,w最大值=1250.
点评:此题主要考查了二次函数的应用以及一次函数的应用,利用分段函数求出是解题关键.

练习册系列答案
相关题目
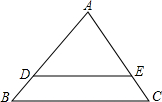 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在直角坐标系xOy中,一次函数y=
x+1的图象与二次函数y=-x2+
x+1的图象交于点A、B,则锐角∠ABO的正弦值等于( )
| 1 |
| 2 |
| 9 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
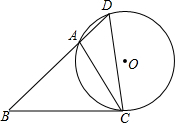 如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆
如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆 如图,AD为△ABC的角平分线,BF⊥AD的延长线于点F,AM⊥AD于A交BC的延长线于M,FC的延长线交AM于E.求证:AE=EM.
如图,AD为△ABC的角平分线,BF⊥AD的延长线于点F,AM⊥AD于A交BC的延长线于M,FC的延长线交AM于E.求证:AE=EM.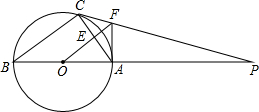 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF. 如图,已知∠AOB=50°,OC平分∠AOB
如图,已知∠AOB=50°,OC平分∠AOB