题目内容
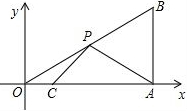 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:作A关于OB的对称点D,过D作DC⊥OA于C,此时PA+PC的值最小,根据三角形相似的性质求出CD,即可得出答案.
解答: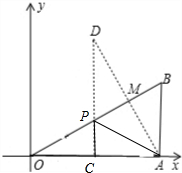 解:作A关于OB的对称点D,过D作DC⊥OA于C交OB于P,
解:作A关于OB的对称点D,过D作DC⊥OA于C交OB于P,
则此时PA+PC=的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(4,3),
∴OB=5,
∵∠AMB=∠OAB=90°,∠ABM=∠OBA,
∴△ABM∽△OBA,
∴
=
,
∴AM=
=
,
∴AD=
,
∵∠DAC+∠MAB=∠B+∠MAB=90°,
∴∠DAC=∠B,
∵∠DCA=∠AMB=90°,
∴△ADC∽△ABM,
∴
=
,
即
=
,
解得CD=
.
 解:作A关于OB的对称点D,过D作DC⊥OA于C交OB于P,
解:作A关于OB的对称点D,过D作DC⊥OA于C交OB于P,则此时PA+PC=的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(4,3),
∴OB=5,
∵∠AMB=∠OAB=90°,∠ABM=∠OBA,
∴△ABM∽△OBA,
∴
| AM |
| OA |
| AB |
| OB |
∴AM=
| 4×3 |
| 5 |
| 12 |
| 5 |
∴AD=
| 24 |
| 5 |
∵∠DAC+∠MAB=∠B+∠MAB=90°,
∴∠DAC=∠B,
∵∠DCA=∠AMB=90°,
∴△ADC∽△ABM,
∴
| DC |
| AM |
| AD |
| AB |
即
| DC | ||
|
| ||
| 3 |
解得CD=
| 96 |
| 25 |
点评:本题考查了轴对称-最短路线问题,勾股定理,三角形相似的判定和性质,关键是求出P点的位置,题目比较好,难度适中.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
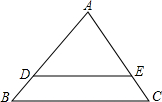 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在直角坐标系xOy中,一次函数y=
x+1的图象与二次函数y=-x2+
x+1的图象交于点A、B,则锐角∠ABO的正弦值等于( )
| 1 |
| 2 |
| 9 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点C是线段AB的一个三等分点,D在CB上,CD:DB=9:1,且CD-AC=2,求线段AB的长.
如图,点C是线段AB的一个三等分点,D在CB上,CD:DB=9:1,且CD-AC=2,求线段AB的长.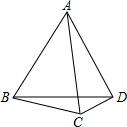 如图,在△ABC中,AB=AC,∠ABC>60°,∠ABD=60°,且∠ADB=90°-
如图,在△ABC中,AB=AC,∠ABC>60°,∠ABD=60°,且∠ADB=90°- 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=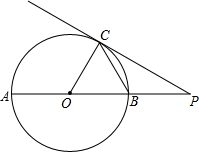 如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.
如图,P是⊙O直径AB延长线上的一点,PC切⊙O于点C,∠P=30°,⊙O的半径长为6.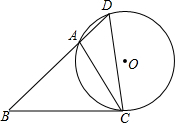 如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆
如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆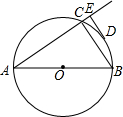 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )