题目内容
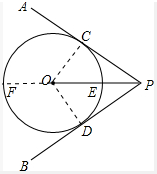
 如图,点O在∠APB的平分线上,圆O与PA相切于点C.
如图,点O在∠APB的平分线上,圆O与PA相切于点C.(1)求证:直线PB与圆O相切;
(2)PO与圆O交于点E.若PE=2,PC=4.求圆O的半径长.
考点:切线的判定与性质
专题:
分析:(1)连接OC,作OD⊥PB于D,先证OC⊥PA,再由O在∠APB的平分线上,证出OD=OC即可;
(2)根据切割线定理得出PC2=PE•PF,求出PF,再求出EF,即可得出半径OE.
(2)根据切割线定理得出PC2=PE•PF,求出PF,再求出EF,即可得出半径OE.
解答:(1)证明:连接OC,作OD⊥PB于D;如图所示:
 ∵PA是圆O的切线,
∵PA是圆O的切线,
∴OC⊥PA,
∵O在∠APB的平分线上,
∴OD=OC,
∵OE⊥PB,
∴直线PB与圆O相切;
(2)解:延长PO交圆O于点F;
根据切线长定理得:PC2=PE•PF,
即42=2×PF,∴PF=8,
∴EF=PF-PR=6,
∴OE=
EF=3;
即圆O的半径为3.
 ∵PA是圆O的切线,
∵PA是圆O的切线,∴OC⊥PA,
∵O在∠APB的平分线上,
∴OD=OC,
∵OE⊥PB,
∴直线PB与圆O相切;
(2)解:延长PO交圆O于点F;
根据切线长定理得:PC2=PE•PF,
即42=2×PF,∴PF=8,
∴EF=PF-PR=6,
∴OE=
| 1 |
| 2 |
即圆O的半径为3.
点评:本题考查了切线的性质与判定以及切割线定理的综合运用;熟练掌握切线的判定和切割线定理是解题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
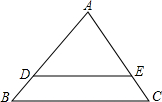 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知二次函数y=x2+3x+m(m为常数)的图象与x轴有两个交点,其中一个交点为(-1,0),则另一个交点是( )
| A、(1,0) |
| B、(2,0) |
| C、(-2,0) |
| D、(-3,0) |
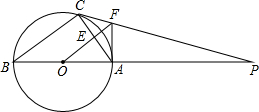 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.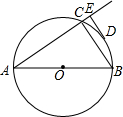 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( ) 如图,已知∠AOB=50°,OC平分∠AOB
如图,已知∠AOB=50°,OC平分∠AOB 如图,△AOB中,A、B两点的坐标分别为(3,4),(6,2).
如图,△AOB中,A、B两点的坐标分别为(3,4),(6,2).